В прямоугольной: В прямоугольной трапеции АВСД из вершины тупого угла ВСД на сторону АД опущен перпендикуляр СЕ….

Расстановка мебели в прямоугольной комнате, правила расстановки мебели в узких и длинных комнатах — фото | Советы по выбору мебели от Столплит

Чаще всего комнаты в наших квартирах имеют прямоугольную форму, о чем нередко сожалеют дизайнеры не особо жалующие прямоугольные помещения. Свидетельством этому может служить тот факт, что прямоугольная комната расстановка мебели фото редко можно увидеть на сайтах агентств и в портфолио дизайнеров.

Содержание:

1. Идеи расстановки мебели на кухне
2. Грамотное расположение мебели в прямоугольной спальне
3. Как лучше разместить мебель в прямоугольной гостиной
4. Необходимая мебель для прямоугольной детской

Идеи расстановки мебели на кухне 

   В прямоугольных кухнях мебель обычно расставляют в один ряд — так называемой прямой планировкой. При таком способе расстановки холодильник, мойка, плита и все шкафчики располагаются вдоль стены.

   Расстановка мебели в длинной комнате таким способом компактна и лаконична, но в этом случае отсутствует удобный для каждой хозяйки рабочий треугольник: холодильник — мойка — плита.

   Также для прямоугольных кухонь при наличии достаточной площади отлично подходит «островное» размещение мебели.        Суть такой расстановки заключается в расположении всех рабочих элементов, не исключая и плиту с мойкой, в центре комнаты, своеобразном острове.

   Такой вариант оптимален для кухонь с большой площадью, для небольших кухонь наиболее подходящим видится вариант с расположением в центе помещения небольшой барной стойки.

Грамотное расположение мебели в прямоугольной спальне

   Расстановка мебели в узкой комнате, в частности в спальне, позволяет визуально расширить ее, не утратив при этом функциональности. Лучшим решением для увеличения объема и пространства комнаты является размещение у короткой стены шкафа высотой от пола до потолка.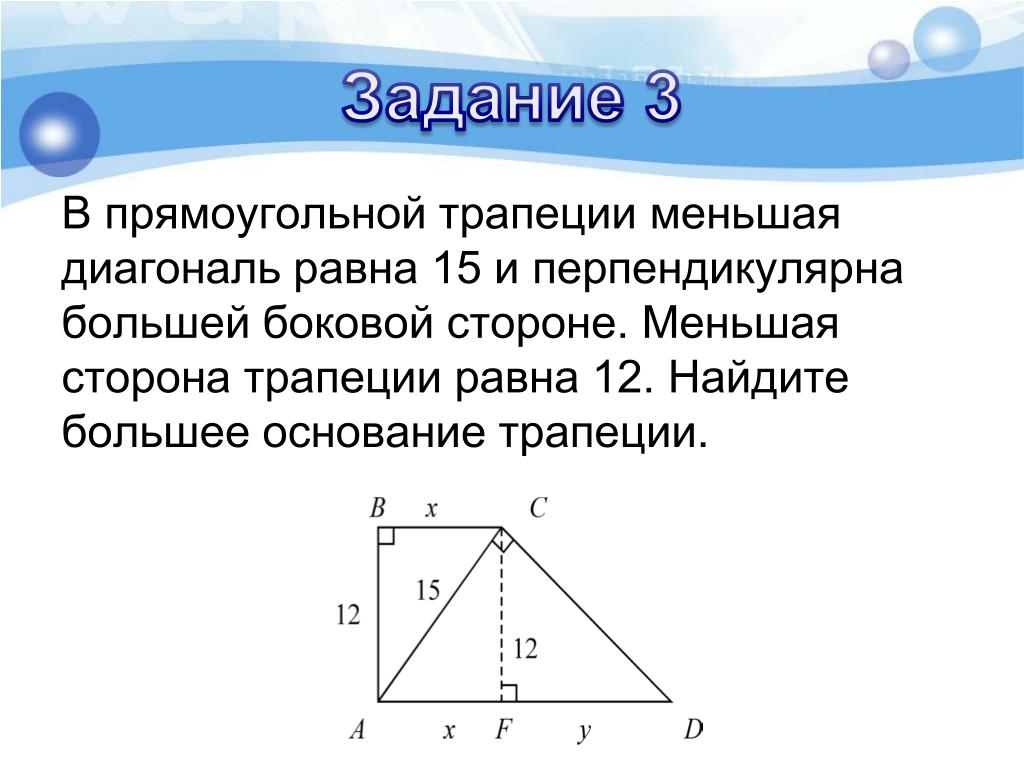 Шкаф создает видимость ложной стены, несколько приближая спальню к форме квадрата. Для расширения пространства прямоугольной спальни отлично подходят зеркала, размещение которых рекомендуется с длинной стороны.

   Для придания ярусности, которая отлично восполняет недостатки узких спален, необходимо повесить полки над столом и над кроватью, что позволит существенно сэкономить место. Полки можно приобрести как готовые, так и изготовить их по индивидуальному заказу.

   Для улучшения зрительного восприятия узкой прямоугольной спальни рекомендуется мебель, устанавливаемую вдоль длинных стен, подбирать немного уже стандартной, меблировка вдоль короткой стены выполняется наоборот, более широкими предметами мебели.

   Расположение кровати в узких спальнях следует продумать в первую очередь. Кровать можно установить у короткой стены напротив более длинных стен, если, конечно, позволяет ширина спальни. Если же этот вариант не подходит, то кровать можно поставить поперек спальни, что даст достаточно места для расстановки других предметов мебели.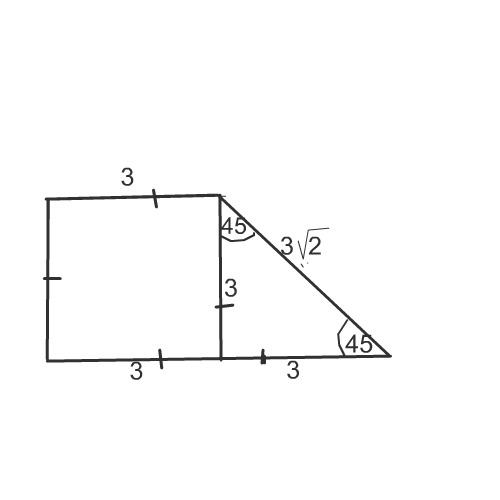

   При расстановке мебели в спальне прямоугольной формы необходимо придерживаться следующих рекомендаций:

• Нельзя устанавливать мебель только вдоль периметра стен комнаты, в результате может создаться неприятное зрительное ощущение длинного коридора;
• При небольшой ширине спальни лучшим вариантом следует считать ассиметричную расстановку мебели;
• Для экономии места кровать можно придвинуть к стене;
• Не следует заполнять узкую спальню излишними декоративными элементами, различными аксессуарами и мелочами — комната будет визуально выглядеть меньшей и захламленной.

Как лучше разместить мебель в прямоугольной гостиной

   Расстановку мебели в прямоугольной гостиной необходимо осуществить таким образом, чтобы было обеспечено максимальное удобство в приеме гостей, проведения семейных торжеств и комфортного вечернего отдыха.

   Прямоугольная форма этой комнаты сама по себе предполагает разделение ее на несколько зон. Зачастую гостиную разделяют на обеденную зону, в которой установлен стол и кресла, и зону, предназначенную для отдыха, где размещают все необходимое для проведения времени всей семьей — мягкую мебель, электрокамин, телевизионную систему. В прямоугольной гостиной кресла и диваны допускается располагать как ближе к середине комнаты, так и вдоль ее стен. При этом необходимо сохранить свободное пространство для удобного перемещения по комнате.

   Для гостиной прямоугольной формы намного предпочтительнее асимметричная меблировка. Мебель лучше всего расставлять либо вдоль длинных стен, либо под прямым углом к ним. 

   В прямоугольных гостиных оптимально создание мебельной группы из углового дивана, журнального столика и нескольких мягких кресел. Центр всей мебельной композиции целесообразно устраивать на длинной стене, таким образом гостиная будет выглядеть «более квадратной».

   При расстановке мебели в прямоугольных помещениях чаще всего допускаются две ошибки:

• Расположение предметов мебели вдоль длинной стены, что приводит к эффекту «коридора».
• Установка всей или большей части мебели в каком-либо углу комнаты, что приводит к ощущению пустоты в оставшемся свободным пространстве и нарушению гармонии мебельной композиции.

Необходимая мебель для прямоугольной детской

   Предметы, располагающиеся в детской комнате, оказывают огромное влияние на формирование вкусов ребенка, развитию его как личности. Потому важно соответствие видов мебели возрасту и уровню развития малыша.

   Главным предметом мебели в детской комнате является кровать, желательно с высокими бортиками. В прямоугольной детской кровать целесообразно устанавливать трансформирующуюся, у которой можно менять размеры при взрослении ребенка. Если детей в семье двое, то оптимальным выбором можно считать двухъярусную кровать, придвинутую к узкой стене. Таким образом срезается длина комнаты и освобождается место для игр.

   Для детей дошкольного возраста необходимо оборудовать игровую зону, расположив натуральный ковер с мягким ворсом, около которого можно разместить шкаф с ящиками для детской одежды и игрушек.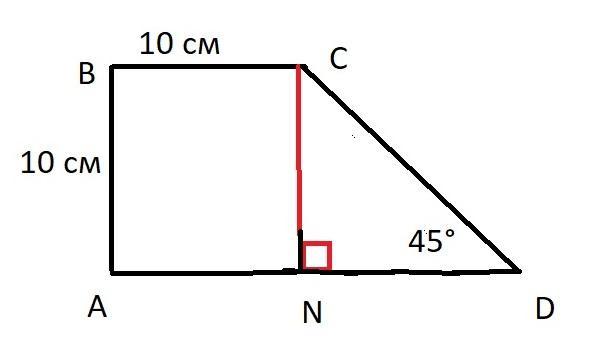

   Письменный стол, за которым малыш будет делать поделки и рисовать, а затем и готовить уроки следует установить поближе к окну — на стол будет попадать больше света. Над столом или рядом с ним необходимы полки для книг и детских аксессуаров.

   Грамотно подобрать мебель можно в нашем интернет-магазине, а расставить ее так, как вам удобно можно в специальной 3D-программе, что сэкономит ваше время и силы.

формулы через стороны, углы, диагонали, площадь

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение высоты прямоугольной трапеции

В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту прямоугольной трапеции.

Напомним, в прямоугольной трапеции одна из боковых сторон перпендикулярна ее основаниями, и потому одновременно является высотой фигуры.

• Нахождение высоты прямоугольной трапеции
  • Через длины сторон
  • Через основания и прилежащий угол
  • Через боковую сторону и прилежащий угол
  • Через диагонали и угол между ними
  • Через площадь и основания

Через длины сторон

Зная длины обоих оснований и большей боковой стороны прямоугольной трапеции, можно найти ее высоту (или меньшую боковую сторону):

Данная формула следует из теоремы Пифагора. В данном случае высота h – это неизвестный катет прямоугольного треугольника, гипотенуза которого равняется d, а известный катет – разности оснований, т.е. (a-b).

Через основания и прилежащий угол

Если даны длины оснований и любой из прилежащих к ним острых углов, то вычислить высоту прямоугольной трапеции можно по формуле:

Через боковую сторону и прилежащий угол

Если известна длина боковой стороны прямоугольной трапеции и прилежащий к ней угол (любой), найти высоту фигуры удастся таким образом:

Примечание: с помощью этой формулы можно, в т. ч., доказать, что меньшая боковая сторона – это и есть высота трапеции:

Через диагонали и угол между ними

При условии, что известны длины оснований прямоугольной трапеции, диагонали и угол между ними, рассчитать высоту фигуры можно так:

Если вместо суммы оснований известна длина средней линии, то формула примет вид:

m – средняя линия, которая равна половине суммы оснований, т.е.m = ^(a+b)/₂.

Через площадь и основания

Если известна площадь прямоугольной трапеции и длина ее оснований (или средней линии), найти высоту можно таким образом:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Что такое прямоугольник? Определение, примеры, формулы, факты

Что такое прямоугольник?

Прямоугольник — это замкнутая двумерная фигура, имеющая 4 стороны, 4 угла и 4 прямых угла (90°). Противоположные стороны прямоугольника равны и параллельны. Поскольку прямоугольник представляет собой двумерную форму, он характеризуется двумя измерениями: длиной и шириной. Длина – это длинная сторона прямоугольника, а ширина – меньшая сторона.

Похожие игры

Прямоугольники вокруг нас

Прямоугольник, являющийся наиболее распространенной формой, является частью нашей повседневной жизни. Некоторые реальные примеры прямоугольника приведены ниже.

Связанные рабочие листы

Как еще мы можем назвать прямоугольник?

• Поскольку все углы прямоугольника равны, мы также называем его равноугольным четырехугольником . Четырехугольник – это четырехсторонняя замкнутая фигура.
  
• Так как прямоугольник имеет параллельные стороны, мы также можем назвать его прямоугольным параллелограммом . Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны. Прямоугольники являются частным случаем параллеграммов.

Что такое диагональ прямоугольника?

Отрезки, соединяющие противоположные углы прямоугольника, называются диагоналями. На данном рисунке две диагонали прямоугольника равны AC и BD. Диагонали прямоугольника имеют одинаковую длину. Следовательно, АС = BD.

Если мы знаем длину и ширину прямоугольника, мы можем использовать теорему Пифагора, чтобы найти длину его диагонали. 9{2}}$

Свойства прямоугольника

Ниже приведены свойства прямоугольника:

1. Это плоская замкнутая форма.
2. Имеет 4 стороны, 4 угла и 4 угла (вершины).
3. Имеет 2 размера, а именно длину и ширину
4. Каждый угол прямоугольника равен 90°.
5. Противоположные стороны равны и параллельны.
6. Имеет 2 диагонали одинаковой длины.

Площадь и периметр прямоугольника

Площадь прямоугольника

Пространство, занимаемое прямоугольником, называется его площадью. Площадь прямоугольника можно вычислить, найдя произведение его длины на ширину. Итак,

Площадь прямоугольника = длина × ширина

Поскольку площадь прямоугольника является произведением длины и ширины, она измеряется в квадратных единицах, например, квадратных метрах (м ² ), квадратных дюймов (в ² ) и так далее.

Периметр прямоугольника

Периметр прямоугольника равен сумме длин его четырех сторон. Найдем формулу периметра прямоугольника.

Периметр прямоугольника = длина + ширина + длина + ширина

                                                                    = 2 (длина + ширина)

Так как мы складываем единицы длины, чтобы найти периметр , его единицей также является 

Периметр измеряется в единицах длины (дюймы, футы, метры и т. д.), потому что мы добавляем длины сторон, чтобы найти ответ.

Интересные факты

1. Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками
2. Диагонали прямоугольника делят прямоугольник на четыре треугольника
3. Каждый квадрат является прямоугольником, но каждый прямоугольник не является квадратом

Решенные примеры на прямоугольнике

1. Определите прямоугольники на данных рисунках.

Решение: 

Фигуры A и D являются прямоугольниками, поскольку у них противоположные стороны равны и параллельны, а все четыре угла прямые.

2. Определите длину, ширину и диагональ данного прямоугольника.

Решение:

Длина → PQ и RS

Ширина → SP и RQ

Диагонали → PR и QS

3. Длина и ширина прямоугольника равны 7 дюймам и 21 дюйм соответственно. Найдите его периметр.

Решение:

Периметр прямоугольника = 2 × (длина + ширина)

                                        = 2 × (7 + 21) дюймов

                                     = 2 × (28) дюймов

                                        = 56 дюймов 9000 7

4. Длина и ширина прямоугольника равны 0,3 м и 15 см. Найдите его площадь.

Решение:

Длина = 0,3 м и Ширина = 15 см

Длина и ширина прямоугольника различны, поэтому преобразуем одну из них. Переведем длину в сантиметры, умножив ее на 100, потому что 1 м = 100 см. 9{2}} = \sqrt{64+36} = \sqrt{100} = \sqrt{10 ✕ 10}$ = 10 дюймов

Практические задачи на прямоугольнике

1

Какова площадь прямоугольного картона 1 м в длину и 30 см в ширину?

30 кв. см

300 кв. см

3 000 кв. см

30 000 кв. см

Правильный ответ: 3 000 кв. см
Длина картона = 1 м = 1 00 см и ширина = 30 см
Площадь прямоугольного картона = 100 см ✕ 30 см = 3000 кв. см

2

Чему равен периметр прямоугольника длиной 16 футов и шириной 7 футов?

23 фута

46 футов

112 футов

305 футов

Правильный ответ: 46 футов
Периметр = 2 × (16 + 7) см = 2 × 23 фута = 46 футов 9 0007 3

Что такое ширина прямоугольника, длина и площадь которого равны 8 см и 32 см2 соответственно?

256 см

4 см

40 см

80 см

Правильный ответ: 4 см
Площадь = длина × ширина
Итак, ширина = площадь ÷ длина прямоугольника = 32 ÷ 8 = 4 см.

Часто задаваемые вопросы о прямоугольнике

Что такое прямоугольник?

Прямоугольник — это замкнутая двумерная фигура, имеющая 4 стороны, 4 угла и 4 прямых угла (90°). Противоположные стороны прямоугольника равны и параллельны.

Какие есть реальные примеры прямоугольников?

Некоторые примеры прямоугольников из реальной жизни включают книги, дверь, столешницу, доску и т. д.

Чем прямоугольник отличается от параллелограмма.

Все стороны квадрата равны, тогда как противоположные стороны прямоугольника равны и параллельны.

Почему все прямоугольники не квадраты?

Все прямоугольники не являются квадратами, потому что по определению прямоугольника его противоположные стороны должны быть равны, но его соседние стороны могут быть или могут быть равными. Таким образом, только прямоугольники с равными смежными сторонами являются квадратами.

Экспертное репетиторство по математике в Великобритании

Прямоугольник — это четырехугольник, у которого все углы равны, а противоположные стороны равны и параллельны. Вокруг нас много прямоугольных объектов. Каждый прямоугольник

формы характеризуется двумя размерами: длиной и шириной. Более длинная сторона прямоугольника известна как длина, а более короткая сторона известна как ширина. В этой главе мы узнаем о форме прямоугольника, некоторых формулах прямоугольника, типах прямоугольников и их свойствах.

1.	Что такое прямоугольник?
2.	Свойства прямоугольника
3.	Диагональ прямоугольника
4.	Площадь прямоугольника
5.	Периметр прямоугольника
6.	Часто задаваемые вопросы о прямоугольнике

Что такое прямоугольник?

Прямоугольник представляет собой замкнутую двумерную фигуру с четырьмя сторонами. Противоположные стороны прямоугольника равны и параллельны друг другу, а все углы прямоугольника равны 90°. Посмотрите на прямоугольник, приведенный ниже, чтобы увидеть его форму, стороны и углы.

Определение прямоугольника

Определение прямоугольника гласит, что прямоугольник представляет собой двумерную фигуру с 4 сторонами, 4 вершинами и 4 внутренними прямыми углами. Противоположные стороны прямоугольника равны и параллельны.

Длина и ширина прямоугольника

Длина прямоугольника относится к большей стороне, а ширина прямоугольника относится к меньшей стороне. Следует отметить, что длину прямоугольника можно вычислить, если известны площадь, периметр и ширина прямоугольника. Точно так же можно рассчитать ширину прямоугольника, если известны площадь, периметр и длина прямоугольника.

Свойства прямоугольника

Прямоугольник – это замкнутая фигура, имеющая четыре стороны и угол, образованный смежными сторонами, равен 90°. Прямоугольник может иметь широкий спектр свойств. Некоторые из важных свойств прямоугольника приведены ниже.

• Прямоугольник — это четырехугольник.
• Противоположные стороны прямоугольника равны и параллельны друг другу.
• Внутренний угол прямоугольника при каждой вершине равен 90°.
• Сумма всех внутренних углов равна 360°.
• Диагонали делят друг друга пополам.
• Длины диагоналей равны.
• Длину диагоналей можно получить с помощью теоремы Пифагора. Длина диагонали со сторонами a и b равна, диагональ = √( a ² + b ² ).
• Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
• Все прямоугольники являются параллелограммами, но не все параллелограммы являются прямоугольниками.

Формулы прямоугольника

У прямоугольника есть несколько основных формул, которые можно запомнить, чтобы найти отсутствующие или неизвестные значения. Несколько формул прямоугольников приведены ниже:

• Формула площади прямоугольника: Если мы знаем длину и ширину прямоугольника, мы можем найти площадь, используя формулу Площадь прямоугольника = Длина × Ширина
• Формула периметра прямоугольника: Если мы знаем длину и ширину прямоугольника, мы можем найти периметр, используя формулу Периметр прямоугольника = 2 (длина + ширина)
• Длина прямоугольника формула: Если мы знаем площадь и ширину прямоугольника, мы можем найти длину , используя формулу площади, подставив значения, или мы можем перефразировать формулу площади следующим образом: длина = площадь прямоугольника ÷ ширина. Точно так же, если мы знаем периметр и ширину прямоугольника, мы можем найти длину , используя формулу периметра, подставив значения, или мы можем переформулировать формулу периметра как Длина = (Периметр ÷ 2) — Ширина
• Формула ширины прямоугольника: Если мы знаем площадь и длину прямоугольника, мы можем найти ширину , используя формулу площади, подставив значения, или мы можем переформулировать формулу площади следующим образом: Ширина = Площадь прямоугольника ÷ Длина. Точно так же, если мы знаем периметр и длину прямоугольника, мы можем найти ширину , используя формулу периметра, подставив значения, или мы можем перефразировать формулу периметра как, Ширина = (Периметр ÷ 2) — Длина

Диагональ прямоугольника

Диагональ прямоугольника — это отрезок, соединяющий любые две его несмежные вершины. В следующем прямоугольнике AC и BD — диагонали, имеющие одинаковую длину. Диагональ делит прямоугольник на 2 прямоугольных треугольника, в которых диагональ образует гипотенузу, а две смежные стороны прямоугольника образуют две другие стороны треугольника.

Диагональ прямоугольника Формула

Формула диагонали прямоугольника выводится с помощью теоремы Пифагора. Следуя приведенному выше рисунку, рассмотрим прямоугольник длины l и ширины w. Пусть длина каждой диагонали равна d. Применяя теорему Пифагора к треугольнику ABD, d ² = l ² + w ² . Извлекая квадратный корень с обеих сторон, √(d ² ) = √(l ² + w ² ). Таким образом, формула диагонали прямоугольника равна диагонали (d): √(l² + w²) и, таким образом, диагонали прямоугольника можно вычислить, когда длина и ширина прямоугольника известны.

Диагональ прямоугольника (d) = √(l² + w²)

Площадь прямоугольника

Площадь прямоугольника — это количество единичных квадратов, которые могут поместиться в прямоугольник. Другими словами, пространство, занимаемое прямоугольником, является площадью прямоугольника. Некоторыми примерами прямоугольных форм являются плоские поверхности мониторов ноутбуков, классных досок, холста для рисования и т. д. Мы можем использовать формулу площади прямоугольника, чтобы найти пространство, занимаемое этими объектами. Например, давайте рассмотрим прямоугольник длиной 4 дюйма и шириной 3 дюйма. Нарисуем единичные квадраты внутри прямоугольника. Каждый единичный квадрат представляет собой квадрат длиной 1 дюйм. Теперь подсчитайте количество единичных квадратов на рисунке ниже. Сколько квадратов вы можете наблюдать? Всего 12 квадратов. Мы уже знаем, что площадь измеряется в квадратных единицах. Поскольку единица измерения этого прямоугольника дана в дюймах, площадь измеряется и записывается в квадратных дюймах. Таким образом, площадь прямоугольника = 12 квадратных дюймов. Таким образом, площадь прямоугольника можно вычислить, зная его стороны (длину и ширину).

Формула площади прямоугольника

Формула площади прямоугольника , длина и ширина (ширина) которого равны «l» и «w» соответственно, является произведением его длины и ширины, то есть:

Площадь прямоугольника = (l × w)

Периметр прямоугольника

Периметр прямоугольника — это длина всей границы прямоугольника. Его можно принять как сумму общей меры длины и ширины прямоугольника, и он выражается в линейных единицах, таких как сантиметры, дюймы и так далее. Например, если вам нужно украсить рамку прямоугольного блокнота, вы можете легко рассчитать, сколько ленты вам понадобится, найдя периметр, или если вам нужно поставить забор вокруг вашего сада, периметр сада даст вам точную длину провода, который вам понадобится. Формула, используемая для вычисления периметра прямоугольника, объясняется ниже.

Формула периметра прямоугольника

Формула для периметра ‘P’ прямоугольника, длина и (ширина) ширина которого равны ‘l’ и ‘w’ соответственно, равна 2(l + w).

Формула периметра прямоугольника = 2 (длина + ширина)

Типы прямоугольников

Четырехугольник, у которого противоположные стороны равны, а смежные стороны пересекаются под углом 90°, называется прямоугольником. У прямоугольника две равные диагонали. Длина диагоналей рассчитывается с использованием длины и ширины.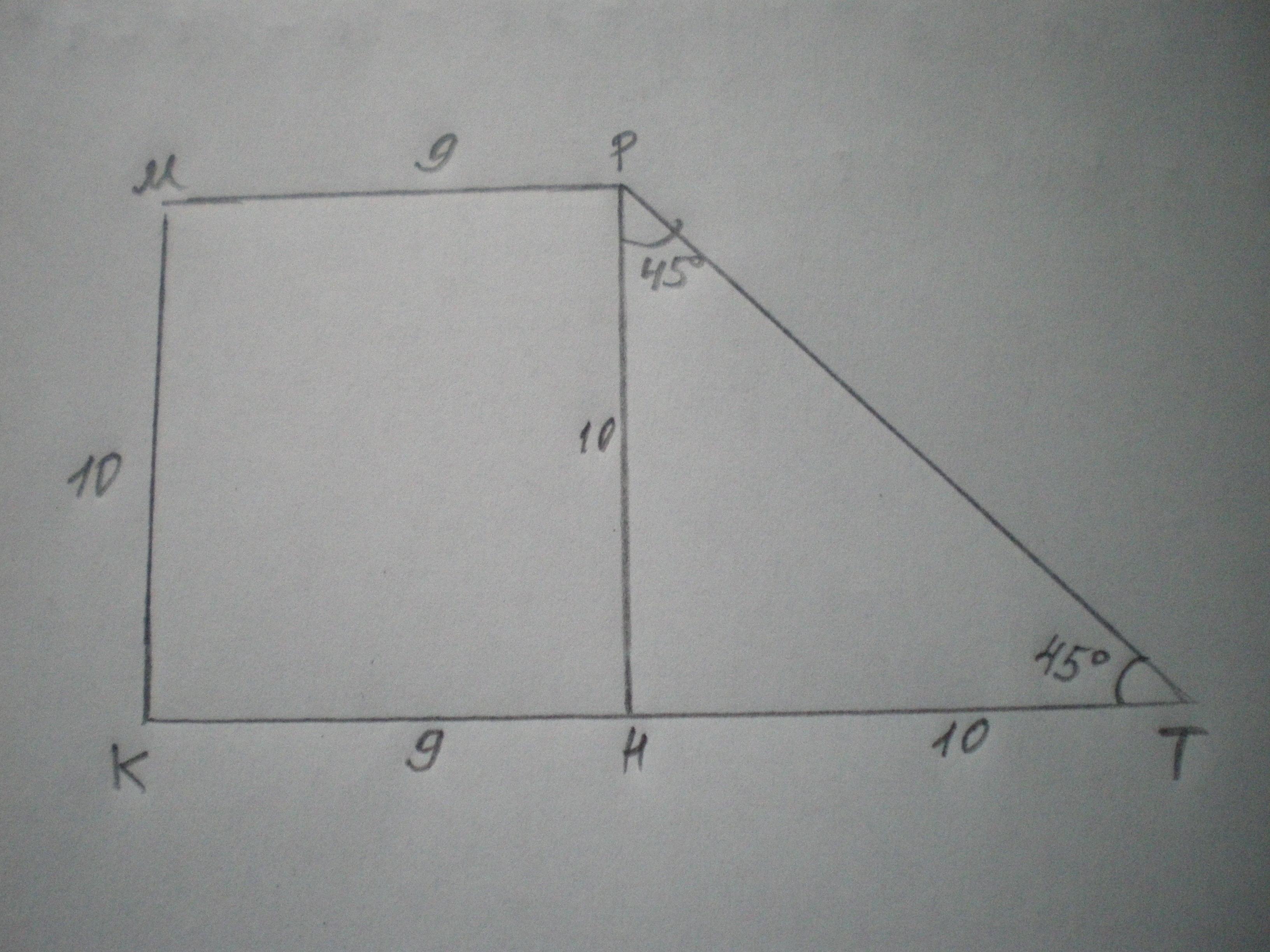 Есть два типа прямоугольников:

• Квадрат
• Золотой прямоугольник

Квадрат

Квадрат представляет собой замкнутую двумерную фигуру с четырьмя равными сторонами и четырьмя равными углами. Это тип прямоугольника, у которого все четыре стороны равны. Внутренний угол в каждой вершине равен 90º, что соответствует определению прямоугольника. Обратите внимание на приведенный ниже квадрат, который соответствует всем свойствам прямоугольника.

Золотой прямоугольник

Золотой прямоугольник — это прямоугольник, отношение длины к ширине которого аналогично золотому сечению, 1: (1+⎷5)/2. Его стороны определены по золотому сечению, то есть 1:1,618. Например, если ширина составляет около 1 фута, тогда длина будет равна 1,168 фута.

☛ Похожие статьи

• Свойства прямоугольника
• Разница между квадратом и прямоугольником
• Является ли квадрат прямоугольником?

Часто задаваемые вопросы о прямоугольнике

Что такое прямоугольник в геометрии?

Прямоугольник представляет собой двумерную фигуру (2D-форму), в которой противоположные стороны параллельны и равны друг другу, а все четыре угла прямые.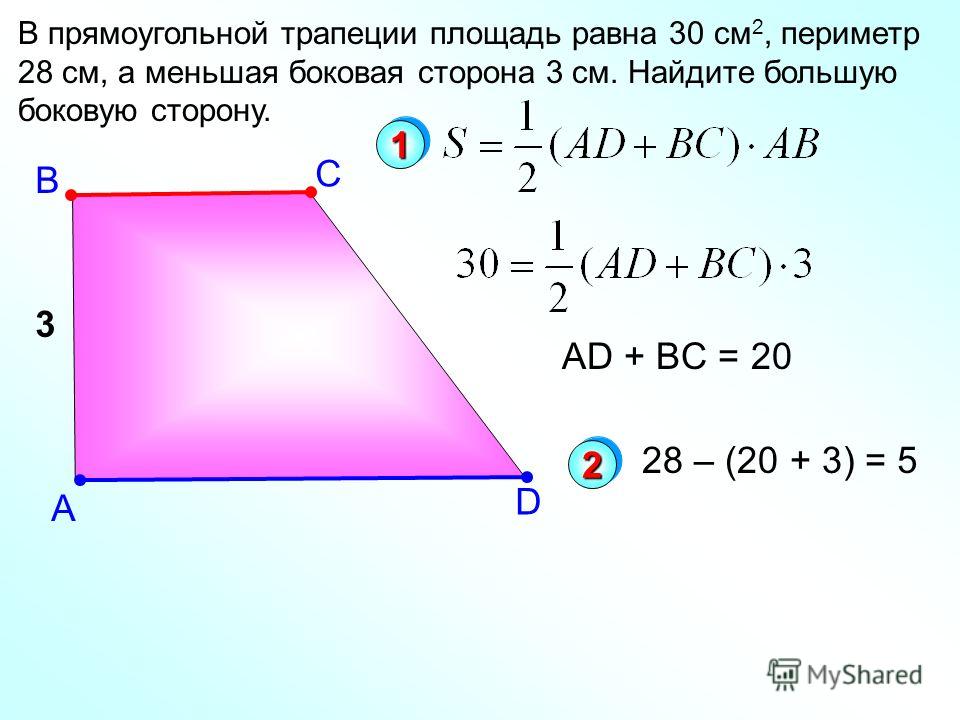 Меньшая сторона прямоугольника называется его шириной (шириной), а длинная сторона – длиной. Одной из самых распространенных геометрических фигур, с которыми мы сталкиваемся в повседневной жизни, является прямоугольник.

☛ Читайте также

• 3D-фигуры
• Геометрические фигуры

Как найти длину прямоугольника?

• Длину прямоугольника можно вычислить, если известны периметр и ширина. Например, если периметр прямоугольника равен 32 единицам, а его ширина равна 4 единицам, мы можем использовать формулу периметра, чтобы получить длину. Периметр прямоугольника = 2 (l + w). Подставим известные значения в формулу, 32 = 2 (длина + 4). Решив это, мы получим длину + 4 = 16, то есть длину = 12 единиц. Точно так же, если площадь прямоугольника и ширина известны, длину можно рассчитать, используя формулу площади прямоугольника и подставив известные значения.
• Другой способ найти длину прямоугольника — использовать следующие формулы, полученные из формул площади и периметра: длина = площадь прямоугольника ÷ ширина; и Длина = (Периметр ÷ 2) — ширина

Как найти ширину прямоугольника?

• Ширину прямоугольника можно вычислить, если известны площадь и длина. Например, если площадь прямоугольника составляет 48 единиц, а его длина — 12 единиц, мы можем использовать формулу площади, чтобы получить ширину. Площадь прямоугольника = l × w. Подставим известные значения в формулу, 48 = 12 × ширина. Решив это, мы получим ширину = 48/12, то есть ширину = 4 единицы. Точно так же, если периметр прямоугольника и длина известны, ширину можно рассчитать, используя формулу для периметра прямоугольника и подставив известные значения.
• Другой способ найти ширину прямоугольника — использовать следующие формулы, полученные из формул площади и периметра: Ширина = Площадь прямоугольника ÷ Длина; и Ширина = (Периметр ÷ 2) — Длина

Как найти диагональ прямоугольника?

Длину диагонали прямоугольника можно вычислить, если известны длина и ширина. Поскольку диагональ прямоугольника образует со своими сторонами прямоугольный треугольник, диагональ становится гипотенузой, и ее значение можно вычислить с помощью теоремы Пифагора. Например, если длина прямоугольника равна 4 единицам, а ширина равна 3 единицам, мы можем найти длину диагонали, используя формулу, диагональ (d) = √ (л² + ш²). Итак, подставим в него значение длины и ширины. Диагональ (d) = √ (l² + w²) = √ (4² + 3²) = √ (16 + 9) = √ 25 = 5 единиц.

Почему прямоугольник не является правильным многоугольником?

Правильный многоугольник — это многоугольник, у которого все стороны имеют одинаковую длину и все углы имеют одинаковую величину. В прямоугольнике только противоположные стороны имеют одинаковую длину, следовательно, прямоугольник не является правильным многоугольником.

☛ Также проверьте:

• Типы полигонов
• Площадь полигонов

Какая формула площади прямоугольника?

Площадь прямоугольника — это площадь, занимаемая им. Площадь прямоугольника равна произведению его длины на ширину (ширину). Формула вычисления площади прямоугольника: Площадь = L × B; где (L) — длина, а (B) — ширина (ширина) прямоугольника.

☛ Ознакомьтесь со списком формул для простых вычислений:

• Формулы периметра
• Объемные формулы
• Формулы площади поверхности
• Формулы измерения

Каковы свойства прямоугольника?

Основные свойства прямоугольника следующие:

• Противоположные стороны параллельны и равны.
• Все углы равны 90°.
• Диагонали равны и делят друг друга пополам.

Площадь прямоугольника равна площади квадрата?

Нет, площадь квадрата не обязательно равна площади прямоугольника, потому что каждый квадрат является прямоугольником, но не все прямоугольники являются квадратами. Формула для вычисления площади прямоугольника: площадь прямоугольника = длина × ширина, а площадь квадрата = (сторона) ² .

Как найти периметр прямоугольника?

Периметр прямоугольника в два раза больше суммы его длины и ширины и выражается по формуле Периметр = 2 (Длина + Ширина). Он выражается в линейных единицах, таких как см, дюймы и т. д.

Как называется трехмерный прямоугольник?

Трехмерный прямоугольник называется прямоугольной призмой. Прямоугольная призма – это призма, основания которой также являются прямоугольниками. Всего у него 6 граней, из которых 3 пары одинаковых противоположных граней, т. е. в прямоугольной призме все противоположные грани одинаковы.