Внешний угол треугольника. Теорема о внешнем угле • Образавр
Содержание
Мы привыкли рассматривать треугольники, в особенности их углы, только «изнутри». Однако, знаете ли, «снаружи» треугольника тоже кипит жизнь. В этом уроке предлагаем узнать, что в геометрии треугольников имеется также внешний угол. А что же такое внешний угол? Какие свойства внешнего угла треугольника существуют? Может, есть какая-нибудь теорема о внешнем угле треугольника? Вот, сейчас будем все выяснять.
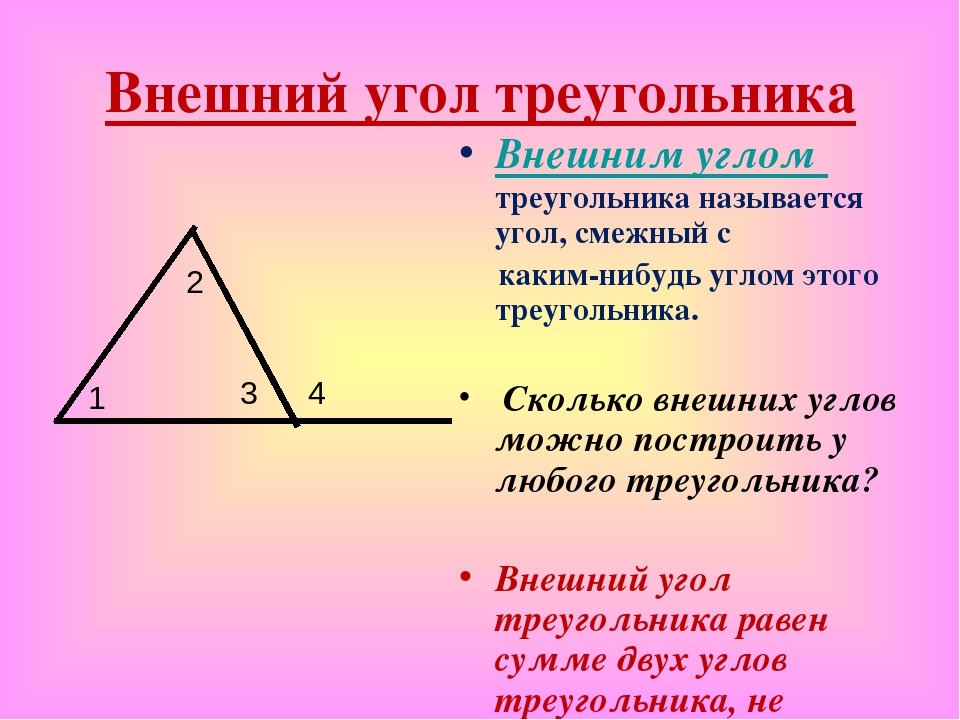
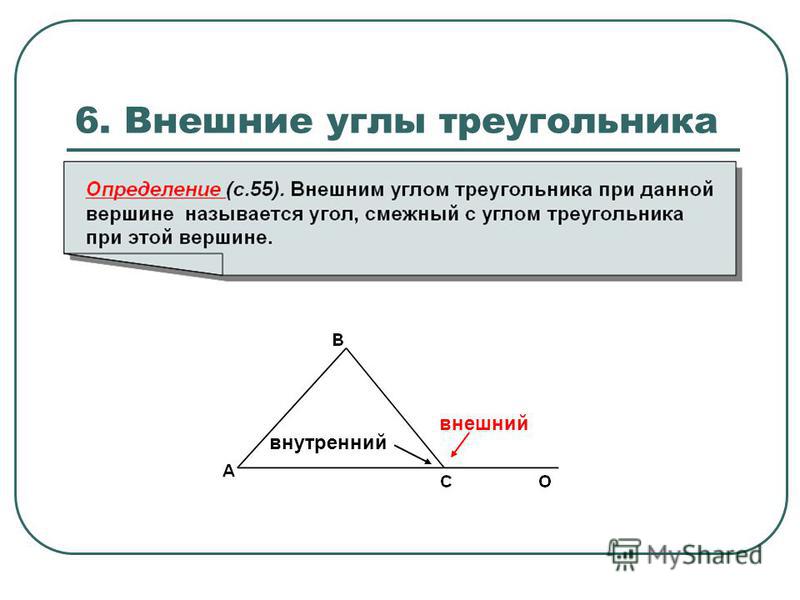
Что такое внешний угол?Начертим треугольник $\bigtriangleup{ABC}$ и построим при вершине $B$ угол, смежный с $\angle{B}$. Теперь в $\bigtriangleup{ABC}$ при вершине $B$ появилось два угла — один «внутри», другой «снаружи». Угол «снаружи» называется внешним углом при вершине $B$. Дадим ему определение.
Как обозначается внешний угол?Внешний угол при данной вершине — угол, смежный с углом треугольника при этой вершине.

Углы в треугольнике обозначаются согласно вершинам, где они располагаются, либо по трем точкам.
Например, в треугольнике $\bigtriangleup{ABC}$ угол при вершине $B$ обозначается как $\angle{B}$, либо как $\angle{ABC}$. А если при вершине $B$ в том числе имеется внешний угол? Его тоже обозначать как $\angle{B}$?
Или лучше указать дополнительную точку на продолжении стороны? Вопрос отличный. Для того, чтобы подобной путаницы не возникало, в геометрии принят термин «внутренний угол».
К примеру, в ходе задачи или доказательства вы пользуетесь внешним углом при некоторой вершине. Скажем, вновь при вершине $B$ в треугольнике $\bigtriangleup{ABC}$. Когда вы ссылаетесь к углу треугольника внутри, можно уточнить: «Внутренний угол $\angle{B}$».
Когда ссылаетесь к углу снаружи, уточняйте: «Внешний угол $\angle{B}$».
Способ с уточнениями «внутренний угол», «внешний угол» проще и не требует дополнительных точек. К тому же, такое обозначение облегчает понимание, где в треугольнике располагается угол. Ведь вы акцентируете внимание только на вершине.
Такое особенно полезно, когда решения или чертежи к задачам громоздкие. Бывает, что при одной вершине нужно рассматривать два внешних угла. Они все равно равны как вертикальные, но все же… Мало ли. Тут удобнее дать углам обозначение в стиле «$\angle{1}$» или, например, «$\angle{x}$».
{"questions":[{"content":"[[image-1]] В треугольнике $\\bigtriangleup{AHF}$ при вершине $A$ построен внешний угол. Как этот угол можно обозначить? Выберите <i><b>все</b></i> подходящие варианты. [[choice-5]]","widgets":{"image-1":{"type":"image","url":"https://obrazavr.ru/wp-content/uploads/2022/04/test-O.svg"},"choice-5":{"type":"choice","options":["$\\angle{A}$","Внешний $\\angle{A}$","$\\angle{OAH}$","$\\angle{OAF}$"],"answer":[1,2]}}}]}Теорема о внешнем угле треугольникаПрименим наши знания теоремы о сумме углов треугольника к внешним углам. \\circ$»,»answer»:»110″}}}]}
\\circ$»,»answer»:»110″}}}]}
Официально теорему о внешнем угле треугольника впервые доказал Евклид — древнегреческий математик, считающийся «отцом геометрии». Примечательно, что его доказательство не имеет ничего общего с теоремой о сумме углов треугольника — математик воспользовался свойствами углов при параллельных и секущей. Оно в принципе и понятно: Евклид огромное количество времени посвятил изучению параллельных прямых.
В качестве практики и повторения материала по параллельным прямым и секущим мы приводим евклидовое доказательство. Оно очень даже достойно внимания. Итак, посмотрим, как внешний угол треугольника «общается» с параллельными прямыми.
Доказательство
Рассмотрим $\bigtriangleup{ABC}$ с внешним углом при вершине $B$. Проведем через эту вершину луч, параллельный стороне $AC$. Отметим на полученном луче точку $B_1$. На продолжении стороны $AB$ отметим точку $B_2$.
Теперь рассмотрим параллельные отрезки $BB_1$ и $AC$ при секущей $AB$. Внутренний угол $\angle{A}$ и угол $\angle{B_{1}BB_2}$ равны как соответственные. Далее рассмотрим отрезки $BB_1$ и $AC$ при секущей $CB$. Углы $\angle{B_{1}BC}$ и $\angle{ACB}$ равны как накрест лежащие.
Видим, что внешний $\angle{B}$ состоит из суммы внутренних углов $\angle{A}$ и $\angle{C}$. Что и требовалось доказать.
Свойства внешнего угла
Не сказать, что свойства внешнего угла многочисленные. В основном, когда затрагивается внешний угол, для решения задач или доказательства чего-либо хватает теоремы о внешнем угле треугольника. Ну, и смежности внутреннего и внешнего углов.
То есть базового определения.
Правда если к делу подключается биссектриса, свойства внешнего угла, помимо «классических», таки обнаруживаются. Разберем одно наиболее полезное.
Свойство биссектрис внешнего и внутреннего углов треугольника.
\circ$.
Internal and external angles — Wikipedia
Toggle the table of contents 22 languages
- العربية
- বাংলা
- Deutsch
- Español
- Euskara
- فارسی
- 한국어
- हिन्दी
- Bahasa Indonesia
- עברית
- Македонски
- Bahasa Melayu
- ភាសាខ្មែរ
- Polski
- Português
- Română
- Suomi
- தமிழ்
- Taqbaylit
- ไทย
- Українська
- 中文
Edit links
From Wikipedia, the free encyclopedia
«Interior angle» redirects here. For interior angles on the same side of the transversal, see Transversal line.
The corresponding internal (teal) and external (magenta) angles of a polygon are supplementary (sum to a half turn). The external angles of a non-self-intersecting closed polygon always sum to a full turn.Internal and external anglesIn geometry, an angle of a polygon is formed by two adjacent sides.
For a simple (non-self-intersecting) polygon, regardless of whether it is convex or non-convex, this angle is called an internal angle (or interior angle) if a point within the angle is in the interior of the polygon. A polygon has exactly one internal angle per vertex. If every internal angle of a simple polygon is less than a straight angle (π radians or 180°), then the polygon is called convex.
In contrast, an external angle (also called a turning angle or exterior angle) is an angle formed by one side of a simple polygon and a line extended from an adjacent side.[1]: pp. 261-264
Properties[edit]
- The sum of the internal angle and the external angle on the same vertex is π radians (180°).
- The sum of all the internal angles of a simple polygon is π(n−2) radians or 180(n–2) degrees, where n is the number of sides. The formula can be proved by using mathematical induction: starting with a triangle, for which the angle sum is 180°, then replacing one side with two sides connected at another vertex, and so on.

- The sum of the external angles of any simple convex or non-convex polygon, if only one of the two external angles is assumed at each vertex, is 2π radians (360°).
- The measure of the exterior angle at a vertex is unaffected by which side is extended: the two exterior angles that can be formed at a vertex by extending alternately one side or the other are vertical angles and thus are equal.
Extension to crossed polygons[edit]
The interior angle concept can be extended in a consistent way to crossed polygons such as star polygons by using the concept of directed angles. In general, the interior angle sum in degrees of any closed polygon, including crossed (self-intersecting) ones, is then given by 180(n–2k)°, where
n is the number of vertices, and the strictly positive integer k is the number of total (360°) revolutions one undergoes by walking around the perimeter of the polygon. In other words, the sum of all the exterior angles is 2πk radians or 360k degrees. Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles, Prometheus Books, 2012.
External links[edit]
- Internal angles of a triangle
- Interior angle sum of polygons: a general formula — Provides an interactive Java activity that extends the interior angle sum formula for simple closed polygons to include crossed (complex) polygons.
Поэкспериментируйте с формулой для углов между внутренним и внешним прямоугольниками | Джейсон Куанг
Опубликовано в·
Чтение: 4 мин.·
8 октября 2021 г.В процессе проектирования вы иногда помещали прямоугольник внутрь другого прямоугольника. Если один из их углов имеет некоторые значения, скажем, изогнутые, и ваша задача состоит в том, чтобы другой получил идеальную кривую, что бы вы сделали?
Это та ситуация, когда мы должны вычислить точное число?Проблема с масштабированием заключается в том, что оно создает выпуклость, а это может быть не то, что мы хотим видеть.
Выпуклость появляется, когда мы просто дублируем и масштабируем прямоугольник.[Обновление]
После нескольких часов публикации и обмена я получил много интересных отзывов. Была формула, которая казалась решением.
R = r + P
Учитывая, что R был внешним углом, r был внутренним углом, а P был отступом (расстояние между внешним и внутренним прямоугольником) — пример 1 ниже.
Однако, если я увеличу P , формула не сработает. В примере 2 дано R = P , поэтому r = 0?
Эта формула хороша на практике, но R всегда должно быть больше, чем P.
Итак, что вы будете делать, если P больше или равно R ?
Путем некоторых экспериментов я понял, что для того, чтобы не угадывать угловые значения с течением времени, нам нужно вычислять.
Но не волнуйтесь! Это было бы обычным делом, если бы мы установили коэффициент для нашей иерархии типографики. Правильно, все, что нам нужно, это коэффициент .
Чтобы сделать вывод о соотношении , я решил провести несколько экспериментов. Во-первых, я сделал прямоугольник 100 на 100 пикселей и еще один прямоугольник 90 на 90 пикселей поместил внутрь первого. Затем я обнаружил, что добавление значения угла к прямоугольнику 100 пикселей на 8 пикселей, и прямоугольнику 90 пикселей на 5 пикселей выглядит просто отлично.
Вот я и подумал, есть ли между ними какая-то связь? Учитывая R внешний угол, r внутренний угол и x отношение, я сделал следующую формулу:
R = г + х*г
равно
x = (R — r)/r
Поскольку r всегда меньше, чем R , поэтому 9 0024 r пришлось добавить пропорцию, чтобы получилось р .
Затем я поместил значения углов, установленные в предыдущем эксперименте, в формулу, у нас получилось:
x = 3/5
. 7 Р и р. Тогда у нас было:
R = r + 3/5*r
итак R = 8*r/5
Или говоря проще, я разделил 90 024 Р по р . Таким образом, R/r = 8/5 1,6 больше, чем внутренние углы. Давайте проверим соотношение с другими размерами прямоугольника. Я установил значение внутреннего угла равным 6 пикселям и применил соотношение, у меня было 9,6 пикселя. Они выглядели великолепно! Формула также, казалось, работала хорошо независимо от прокладок.
Соотношение, казалось, работало хорошо даже с разными размерами прямоугольников.Но соотношение не работало, если внешние углы были настолько круглыми, что превращали внешний прямоугольник в круг, как в примере ниже.
Внешние углы были настолько круглыми, что внешний прямоугольник почти превратился в круг.Формула может применяться во многих случаях. Когда дело доходит до карточек и кнопки, которые помещаются внутрь другой, мы можем меньше времени решать, какие значения углов будут подходящими.
Конечно, это только то соотношение, которое, как я обнаружил, хорошо работает для меня. Там также должны быть некоторые исследования и формулы, но я хотел бы поделиться своим собственным процессом. Хотя мой английский может иметь некоторые ошибки при написании этого, я ценю ваше чтение.
P/s: Вы можете попробовать другие соотношения, если увидите, что они работают, и напишите в комментариях, какое у вас. Ваше здоровье!
Уплотнение внутреннего/внешнего угла
Уплотнительные уголки Codex представляют собой предварительно изготовленные формованные детали для уплотнения внутренних и внешних углов. Углы соединяются внахлест на уплотнительную ленту codex.
- Технический паспорт
Применение
- Для всех уплотнительных систем Codex
- Для классов нагрузки A, A0, B, B0 и C в соответствии с бюллетенем ZDB
- Для классов водонепроницаемости W0-I, W1-I, W2-I и W3-I согласно DIN 18534
- Для классов водонепроницаемости W1-B и W2-B согласно DIN 18535 (цистерны и контейнеры)
- Для уплотнение балконов, лоджий и проходов согласно DIN 18531-5
- Для балконов и террас с уклоном > 1,5%
- Для душевых, ванн и туалетов
- Для домов престарелых и гостиниц
- Для бассейнов
- Для вода резервуары и цистерны
- Для внутренних и наружных работ
- Для жилых, промышленных и коммерческих помещений
- Для угловых, соединительных и деформационных швов
- На сульфатно-кальциевых и цементных стяжках, бетоне
- На гипсе, известковом цементе и цементной штукатурке
- На гипсокартоне и плиты из гипсокартона, несущие элементы плитки
- На полы с подогревом, на стены и полы
Свойства
- Водостойкие и химически стойкие
- Морозостойкий и жаростойкий
- Легко обрабатывается
- Гибкий
- Толщина материала: 0,7 мм
- Длина стороны: 120 x 120 мм
- Соответствует кодексу Уплотнительная лента
- Высший уровень качества 4 согласно критерию DGNB ENV 1.
2 Риски для местная экология
- EMICODE EC 1 PLUS / очень низкий уровень выбросов
- Для безопасного строительства
Готовые уплотнительные уголки codex подходят для герметизации компонентов, подверженных воздействию влаги во внутренних и наружных помещениях и зонах с химической нагрузкой.
- Загрузка
- Технические характеристики
- Информация для заказа
- Знаки качества
Загрузка
- Технический паспорт 251 KB 9 0189
- Сертификат ЕС 294 KB
Технические характеристики
Тип упаковки коробка
Размер упаковки 25 штук
Срок годности 36 месяцев
Цвет зеленый
Длина 12 см
902 84Ширина 12 см
Толщина ок.

 \circ$.
\circ$. 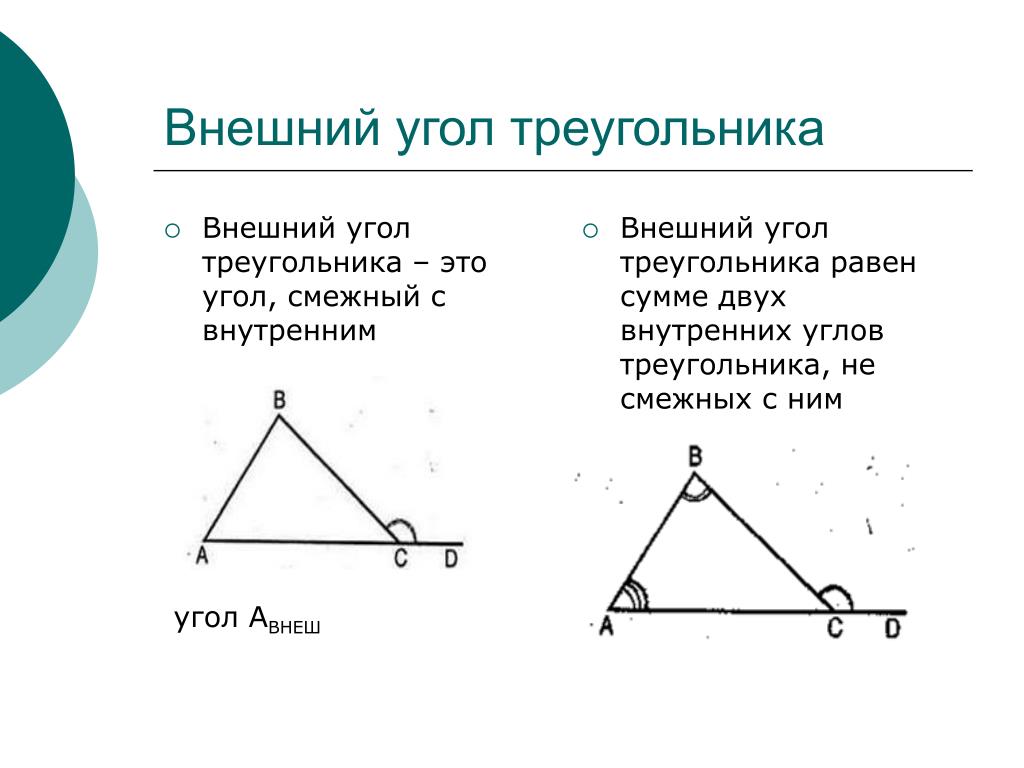
 Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles, Prometheus Books, 2012.
Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles, Prometheus Books, 2012.
 Но не волнуйтесь! Это было бы обычным делом, если бы мы установили коэффициент для нашей иерархии типографики. Правильно, все, что нам нужно, это коэффициент .
Но не волнуйтесь! Это было бы обычным делом, если бы мы установили коэффициент для нашей иерархии типографики. Правильно, все, что нам нужно, это коэффициент . Затем я поместил значения углов, установленные в предыдущем эксперименте, в формулу, у нас получилось:
Затем я поместил значения углов, установленные в предыдущем эксперименте, в формулу, у нас получилось: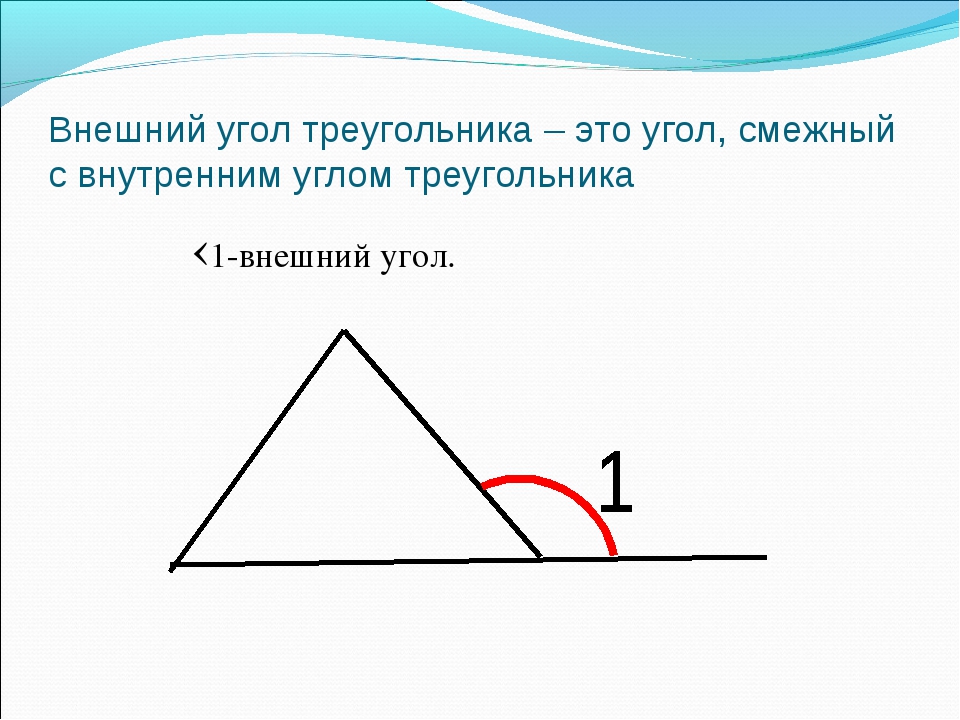

 2 Риски для местная экология
2 Риски для местная экология