Профилированный брус полукруглый: Виды профилированного бруса, технология изготовления

Содержание

Профилированный брус — о нас

ГК «ТВОЙ ДОМ» занимается проектированием и изготовлением готовых дом-комплектов из профилированного бруса, двойного бруса, клееного бруса на специализированном оборудовании, для дальнейшей сборки по нашим чертежам.

Сырье, используемое нами в производстве домов это Ангарская сосна, лиственница и кедр. Плотность дерева очень большая что способствует прочности и долговечности строений. Строительство из дерева приобретает все большую популярность.

Это обусловлено тем, что:

дерево является одним из самых экологически чистых строительных материалов
дерево «дышит» и само поддерживает оптимальный режим влажности воздуха внутри помещения
деревянный дом обойдется вам намного дешевле каменного дома.
строение обеспечивает идеальный климат внутри помещений
служит очень долгое время, и благодаря целительным свойствам дерева, обеспечивает здоровье своим владельцам

вписывается в любой ландшафтный дизайн и, к тому же, будет настоящим произведением искусства.

Мы осуществляем качественный и постоянный контроль всего процесса: от выбора древесины до производства готовых конструкций.

«ГК-ТВОЙ ДОМ.РФ» разработала различные типы профиля бруса, которые удовлетворят даже самых взыскательных заказчиков. У нас представлены: прямой, круглый и полукруглый профили (какой брус мы производим в разделе «профилированный брус»). Конфигурация профилированного бруса представляет собой шип и паз, благодаря этому образуется так называемый «замок», который позволяет прокладывать межвенцовый утеплитель на всю ширину бруса, тем самым обеспечивая стопроцентное утепление стен, исключает попадание влаги, и препятствует образованию щелей.

Современная новая технология двойного бруса с замком «ласточкин хвост» позволяет сделать смежную технологию, главное отличие от проектов из бруса это цена и теплоизоляция такого дома.

Технология клееного бруса так же запускается на нашем производстве с 2021 года.

Новая современная линия склейки досок в брус пользуется большой популярностью, а именно у нас клееный брус из лиственницы, кедра и сосны.

Высокое качество обработки поверхностей профилированного бруса позволяет использовать его без дополнительной отделки внешних и внутренних стен. Профилированный брус отлично подходит для строительства домов, бань, беседок.

ГК «ТВОЙ ДОМ» предлагает своим клиентам проекты из нашего каталога совершенно бесплатно , либо сделает индивидуальный проект.

ГК «ТВОЙ ДОМ» предлагает так же сопутствующие материалы для строительства дома или бани, такие как; вагонка, доска пола, террасная доска, обрезной пиломатериал, джут, перфорированный крепеж, утеплитель и многое другое.

Партнеры ГК «ТВОЙ ДОМ» осуществляют строительство под ключ в таких регионах как: Приморский край, Иркутская область, Новосибирская область , Якутия, Сахалин, Петропавловск-Камчатский и других регионах

У нас выгодно покупать, потому что:

Индивидуальный подход к каждому клиенту.
Возможность проектирования удаленно от клиента.
Осуществление контроля на всех этапах, от проектирования до изготовления дом-комплекта.

Собственное производство профилированного бруса — Мерастрой

Имя *

E-mail *

Ваш вопрос *

Отправляя форму, я принимаю условия конфиденциальности персональной информации, в том числе в части обработки и использования моих персональных данных

Имя *

Телефон для связи

Электронный адрес (e-mail) *

Сообщение *

Компания MERA-STROY оборудовала собственные производственные мощности в Кировской области и наладила там выпуск качественного профилированного бруса, а также сопутствующих пиломатериалов для строительства. Изделия, которые мы выпускаем, позволяют нашим клиентам существенно снизить общие сметные расходы ведь сегодня все будущие домовладельцы старательно ищут пути для удешевления процесса, чтобы не отказываться от него.

Поэтому мы старательно внедряем новые технологии и оборудование, что позволяет добиваться снижении цен на профилированный брус и прочую продукцию. Процесс проводится в несколько этапов.

На мощном станке выпиливается брус определенного размера.
После чего на четырехстороннем станке американской компании Lidermac полученное изделие строгается и профилируется с 4 сторон.
Брус торцуется на детали и маркируется соответственно предназначению стенового материала.
На специализированном обрабатывающем станке проводится нарезание чашек.

Все процессы автоматизированы, включая контроль. Он проводится на всех этапах производства. Человеческий фактор фактически исключается, а потому готовая продукция всегда полностью соответствует проектным размерам.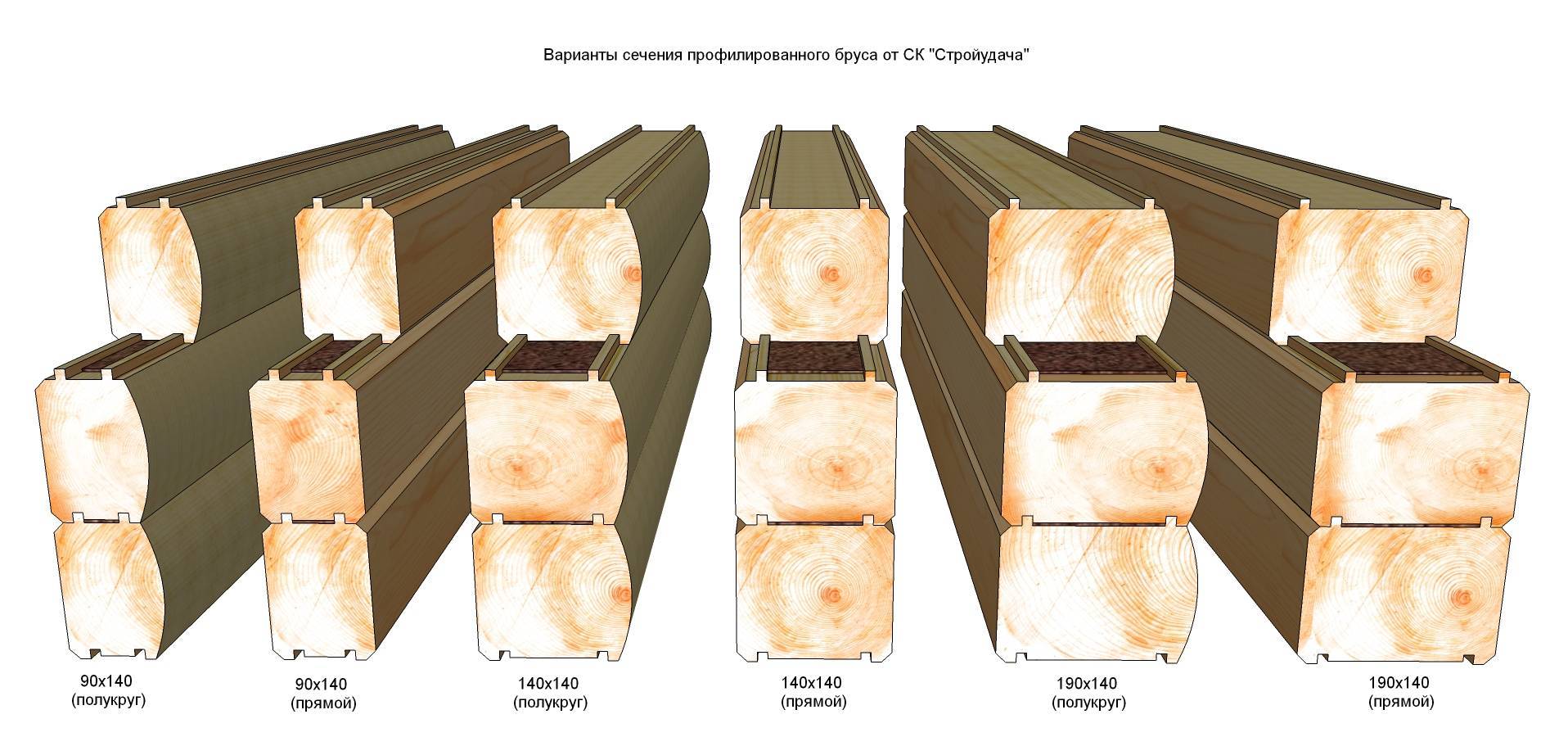

Мы также производим разные виды профилей и замков. Для вашего будущего дома мы предложим недорогие изделия:

прямоугольной формы разных сечений;
под блок-хаус (полукруглый с одной стороны)
шип-паз — финский профиль;
«гребенка».

Наши производственные мощности работают по 7-дневному графику. Это позволяет нам обеспечить постоянный и равномерный выпуск продукции в тех объемах, которые требуются для бесперебойного снабжения всех наших строящихся объектов. Выбирая продукцию нашего производства, вы:

сэкономите бюджет;
быстрее и без проблем расплатитесь с банками, в которых взяли кредит под строительства дома по одному из наших проектов;
ускорите процесс, даже если выбрали поэтапное строительство.

Каждый заказ для нас индивидуален, а потому мы всегда учитываем особенности именно вашего проекта.

На заказ мы изготовим многофункциональные и эксклюзивные аксессуары, которые сделают ваш дом особенным, а проживание – комфортным. Получить подробную консультацию предлагаем по телефону или в режиме онлайн.

Обзор формирования лазерного луча

| Edmund Optics

Это Разделы 5.1, 5.2, 5.3, 5.4, 5.5, и 5.6 Справочника по лазерной оптике.

Предыдущий раздел Следующий раздел

Форма лазерного луча обычно определяется его распределением излучения и фазой. Последнее имеет важное значение для определения однородности профиля пучка по расстоянию его распространения. Поэтому формирователи луча предназначены для перераспределения энергетической освещенности и фазы оптического луча для достижения желаемого профиля луча, который поддерживается на желаемом расстоянии распространения. Распространенные распределения освещенности включают гауссово распределение, при котором облученность уменьшается с увеличением радиального расстояния, и лучи с плоской вершиной, также известные как цилиндрические лучи, в которых облученность постоянна на заданной площади (9).0011 Рисунок 1 ). Подробное описание распространения гауссова луча можно найти в наших указаниях по применению гауссового луча, а информацию о количественной оценке качества распределения излучения лазера можно найти в наших указаниях по применению режимов лазерного резонатора.

Рис. 1: Для профиля пучка Гаусса (слева) освещенность уменьшается с увеличением расстояния от центра в соответствии с уравнением Гаусса. Для плоского верхнего луча (справа) освещенность постоянна на заданной площади.

В некоторых приложениях лучше использовать профили луча, отличные от профилей лазерного источника, которые обычно являются гауссовыми. Например, профили с плоской вершиной выгодны в таких приложениях, как определенные системы обработки материалов, поскольку они часто обеспечивают более точные и предсказуемые разрезы и кромки, чем гауссовые лучи ( рис. 2 ). Однако введение оптики, формирующей луч, увеличивает сложность и стоимость системы.

Рисунок 2: Пучки с гауссовым профилем менее эффективны, чем пучки с плоской вершиной, в приложениях лазерной абляции из-за большой площади луча с избыточной энергией выше требуемого порога абляции и энергии ниже порога во внешних областях гауссова профиля.

Формирование луча изменяет свойства света на их самом фундаментальном уровне, и его эффективность определяется принципом неопределенности Гейзенберга в зависимости от временной полосы: 0007 (1)

$$ \Delta _x \Delta _{\nu} \geq \frac{1}{4 \pi } $$

x представляет положение, а v представляет импульс. Принцип неопределенности накладывает некоторые ограничения на конструкцию формирователей луча. Например, для дизайна с очень четко определенным положением пространственные частоты становятся менее определенными. Применяя принцип неопределенности к теории дифракции, т.е. соотношение преобразования Фурье в интеграле Френеля, получаем характеристический параметр $\beta$:

(2) $$ \beta = C \frac{r_i r_o}{\lambda z} $$

(2)

$$ \beta = C \frac{r_i r_o}{\lambda z} $$ 90 007

, где $ \small{r_o} $ — полуширина входного луча, $ \small{r_i} $ — полуширина выходного луча, $ \small{C} $ — константа, $ \small{\lambda} $ — длина волны, а $ \small{z} $ — расстояние до выходной плоскости. Значение $ \small{\beta} $ очень важно при разработке или рассмотрении приложения для формирования луча, поскольку большие значения соответствуют лучшей производительности формирования луча. Например, при $ \small{\beta} < 4 $ формирователь луча не будет давать приемлемых результатов практически для любого лазерного применения, в то время как $ \small{ 4 < \beta <16} $ обеспечит низкую производительность. Следовательно, для оптимальной работы следует использовать экспериментальные условия, которые приводят к $ \ small{\ beta} > 16 $. Эта формула подразумевает, что будет проще спроектировать формирователи луча для больших лучей, более коротких длин волн и более коротких фокусных расстояний.

Формирование преломляющего луча

В системах с низкой производительностью, где стоимость является определяющим фактором, гауссовы лучи могут быть физически обрезаны апертурой для формирования псевдоплоского верхнего профиля. Это неэффективно и тратит энергию во внешних областях гауссового профиля, но сводит к минимуму сложность и стоимость системы.

В приложениях с более высокими характеристиками, требующих большей эффективности, часто используются преломляющие и дифракционные формирователи лазерного луча. В этих сборках обычно используются фазовые элементы с отображением поля, такие как асферические линзы или линзы произвольной формы и дифракционные элементы, для перераспределения освещенности и фазового профиля лазерного излучения. На рис. 3 показан пример компоновки картографа поля преломления, который преобразует профиль гауссового луча в профиль с плоской вершиной за счет искажения волнового фронта и условия сохранения энергии. ² Амплитуда и фаза падающего луча изменяются после прохождения через оба элемента в линзе Галилея или Кеплера. Полученное в результате формирование луча является высокоэффективным (> 96% пропускной способности) и не зависит от длины волны в пределах диапазона конструкции. Формирователи преломляющего луча обеспечивают равномерное распределение освещенности и плоские фазовые фронты.

Рис. 3: Пример формирования преломляющего луча с использованием карты поля ²

Однако фокусировка луча с плоской вершиной через линзу не приведет к получению профиля плоской вершины в конечном сфокусированном пятне, поскольку линза будет влиять на профиль луча. Когда требуется сфокусированное пятно с плоской вершиной, вместо этого используются преобразователи поля для преобразования гауссовых лучей в коллимированные профили диска Эйри, которые формируют пятна с плоской вершиной после фокусировки бездифракционной линзой ( рис. 4 ).

Рисунок 4: Изображение того, как некоторые формирователи луча, такие как формирователь луча с плоской вершиной AdlOptica Focal-πShaper Q, преобразуют профили падающего гауссова луча в профили воздушного диска, так что они приводят к профилям луча с плоской вершиной после передачи через фокусирующую оптику.

Формирование дифракционного луча

Формирователи дифракционного луча используют дифракцию, а не преломление, для формирования лазерного луча в определенное распределение излучения. Дифракционные элементы используют процесс травления для создания определенной микро- или наноструктуры в подложке. Как правило, проектные длины волн и функция элемента зависят от высоты и расстояния между зонами соответственно. Следовательно, использование дифракционного оптического элемента на расчетной длине волны имеет важное значение, чтобы избежать ошибок в работе. По сравнению с рефракционными формирователями луча дифракционные элементы также больше зависят от выравнивания, расходимости и положения луча в плоскости номинального рабочего расстояния. С другой стороны, дифракционные оптические элементы очень выгодны в лазерных установках с ограниченным пространством, поскольку они обычно состоят из одного элемента, а не из нескольких преломляющих линз.

Интеграторы лазерного луча

Интегратор лазерного луча, или гомогенизатор, состоит из нескольких линз, которые делят луч на массив меньших лучей или лучей, за которыми следует линза или другой фокусирующий элемент, который накладывает лучи на плоскость цели.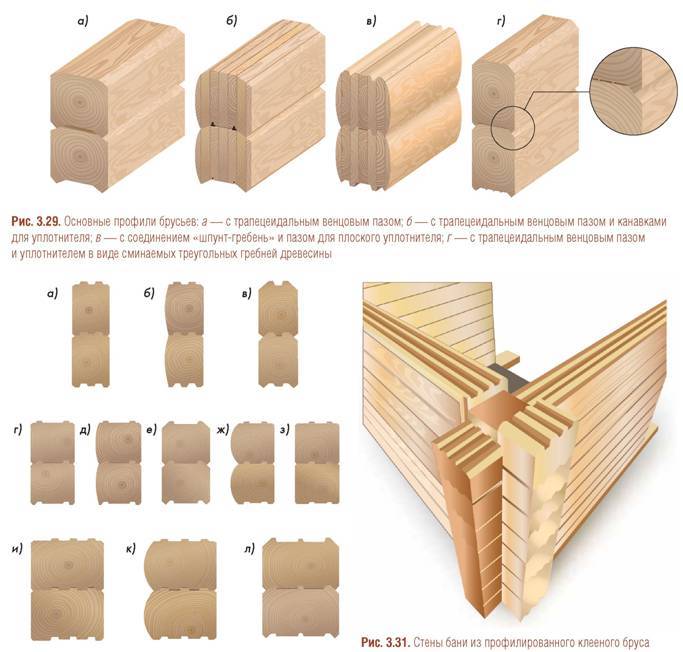 Они могут использоваться как с когерентным лазерным излучением, так и с другими некогерентными источниками света. Как правило, окончательный профиль выходного луча представляет собой сумму картин дифракции, определяемых массивом линз. Большинство интеграторов лазерного луча используются для создания гомогенизированного профиля с плоской вершиной из падающих гауссовых лучей. Гомогенизаторы луча обычно страдают от случайных флуктуаций освещенности, что приводит к не идеально ровному профилю луча. Интеграторы пучков, не основанные на дифракции, такие как интеграторы изображений или волноводы, также подходят для пространственно некогерентного падающего света. Выбор между интеграторами дифракционного или отображающего пучка зависит от числа Френеля. Как правило, при числах Френеля <10 потребуется интегратор изображений для получения очень однородного профиля с плоской вершиной.

	Преломляющий	Дифракционный	Балочные интеграторы
Принцип формирования	Детерминированный	Детерминированный	Случайный или квазислучайный
Случайные колебания	Низкий	Низкий	Высокий
Чувствительность выравнивания	Низкий	Низкий	Высокий
Однородность выходного луча	Высокий	Средний-высокий	Низкий
Стоимость	Высокий	Средний	Низкий
Отпечаток	Большой	Маленький	Маленький

Таблица 1: В этой таблице сравниваются различные технологии формирования лазерного луча.

Axicons для генерации пучков Бесселя

До сих пор мы обсуждали формирование света с помощью картирования поля или интеграции пучков, когда дифракционные эффекты играют главную роль в конструкции и характеристиках оптики. Дифракция — это отклонение света от прямого распространения, не вызванное отражением или преломлением. Эти эффекты дифракции заставляют лазерные лучи расходиться по мере их распространения. С другой стороны, пучок, профиль которого описывается функцией Бесселя, определяемой как точное и инвариантное решение уравнения Гельмгольца, не испытывает дифракции; то есть он не распространяется по мере распространения. ⁴ Эти лучи также являются самовосстанавливающимися, что означает, что они могут восстановиться в любой момент после препятствия. Однако идеальные пучки Бесселя невозможно создать, потому что они требуют бесконечного количества энергии. Вместо этого приближенные лучи Бесселя, известные как квазибесселевые лучи, могут генерироваться интерференцией плоских волн, образованных конической поверхностью, такой как аксикон.

Аксиконы формируют квазибесселев пучок с почти нулевой дифракцией в заданной области, известной как их глубина резкости (DOF). После этой области пучок продолжает распространяться по кольцу (Рисунок 5 ). Традиционными рефракционными аксиконами считаются либо конические линзы, либо призмы. Свет проходит через них, а затем преломляется на конической поверхности. Отражающие аксиконы с отражающей конической поверхностью также используются в определенных ситуациях, например, в сверхбыстрых лазерных системах. Широкая полоса длин волн, присущая сверхбыстрым лазерам, будет испытывать значительную хроматическую дисперсию при передаче через преломляющий аксикон, в то время как в отражающих аксиконах эта дисперсия отсутствует (9).0011 Рисунок 6 ). Квазибесселевские пучки также могут быть получены с использованием голографических методов с высокой эффективностью дифракции, но имеют осевой профиль, модулированный дифракцией.

Рис. 5: Схема традиционного рефракционного аксикона, показывающая область луча Бесселя в ГРИП и кольцеобразный пучок, который распространяется после области перекрытия.

Рис. 6: Схема отражающего аксикона, который, как и традиционный аксикон, создает область луча Бесселя в ГРИП и кольцеобразный пучок после области перекрытия, но, в отличие от традиционных аксиконов, не зависит от длины волны.

Лучи Бесселя почти не претерпевают дифракции на расстоянии распространения и обеспечивают превосходную глубину резкости, что делает их идеальными для таких приложений, как лазерная обработка материалов и хирургия роговицы. Благодаря одинаковому диаметру луча в DOF могут быть получены чистые срезы с острыми кромками.

Круговые лучи с цилиндрическими линзами

Другой тип формирования лазерного луча — круговой, который включает преобразование овального профиля или профиля другой формы в круглый. Лазерные диоды без коллимирующей оптики будут иметь разные углы расходимости по осям x и y из-за прямоугольной формы активной области диода, что приводит к продолговатой форме луча (9).0011 Рисунок 7 ). Круглые профили часто желательны для формирования симметричных, компактных пятен окончательной фокусировки.

Рисунок 7: Геометрия лазерных диодов заставляет их создавать эллиптические лучи с двумя разными углами расхождения

Как и стандартные сферические линзы, цилиндрические линзы используют изогнутые поверхности для схождения или расхождения света, но они обладают оптической силой только в одном измерении. Цилиндрические линзы не влияют на свет в перпендикулярном измерении. Этого нельзя достичь, используя стандартные сферические линзы, потому что свет будет равномерно фокусироваться или рассеиваться вращательно-симметричным образом. Это свойство цилиндрических линз делает их полезными для формирования лазерных световых листов и округления эллиптических лучей.

Система отсчета цилиндрических линз определяется двумя ортогональными измерениями: направлением увеличения и направлением без увеличения. «Направление оптической силы» проходит по изогнутой длине линзы и является единственной осью линзы с оптической силой ( Рисунок 8 ). «Неоптимальное направление» цилиндрической линзы проходит по всей длине линзы без какой-либо оптической силы. Длина цилиндрической линзы вдоль направления без оптической силы может изменяться, не влияя на оптическую силу линзы. Цилиндрические линзы могут иметь различные форм-факторы, включая прямоугольную, квадратную, круглую и эллиптическую формы.

Рис. 8: Направления оптической силы и без оптической силы в прямоугольных и круглых цилиндрических линзах

Поскольку лазерные диоды расходятся асимметрично, сферическую оптику нельзя использовать для получения кругового коллимированного луча от диода. Линза воздействует на обе оси одновременно, что сохраняет исходную асимметрию луча. Каждую ось можно рассматривать отдельно, используя ортогональную пару цилиндрических линз.

Соотношение фокусных расстояний обеих линз должно совпадать с отношением расхождений пучка по осям x и y для достижения симметричного выходного луча. Подобно стандартной коллимации, лазерный диод размещается в общей точке фокуса обеих линз, а расстояние между линзами поддерживается равным разнице их фокусных расстояний ( Рисунок 9 ).

Рис. 9: Пример округления эллиптического луча с помощью цилиндрических линз.

Небольшая выходная апертура лазерных диодов может привести к очень большим углам расходимости, что может вызвать трудности при попытке коллимировать луч. Дивергенция напрямую влияет как на допустимую длину системы, так и на требуемые размеры линз. Взаимосвязь между расходимостью и размером луча описана в наших примечаниях по применению гауссового луча. Поскольку относительные положения каждой цилиндрической линзы достаточно фиксированы в зависимости от их фокусного расстояния, можно рассчитать максимальную ширину луча $ \left( \small{d} \right) $ на каждой линзе, используя фокусное расстояние линзы $ \left( \small{f} \right) $ и угол расхождения $ \left( \small{\theta} \right)$ оси, с которой линза коллимирует. Чистая апертура каждой линзы должна быть больше, чем соответствующая максимальная ширина луча, чтобы избежать ограничения луча.

(3) $$ d = 2 f \times \tan{\left( \frac{\theta}{2} \right)} $$

(3)

$$ d = 2 f \times \tan{\left( \frac{\theta}{2} \right) } $$

Для получения дополнительной информации см. рекомендации по применению цилиндрических линз.

Круговые лучи с парами анаморфотных призм

Пара анаморфотных призм — это другие типы оптики, используемые для круговых эллиптических лучей. Анаморфные пары призм состоят из двух призм, используемых вместе для изменения формы лазерного луча. Обычно они используются для преобразования эллиптических профилей луча в круговые распределения, но они также могут создавать другие эллиптические профили луча различных размеров. Оптический принцип изменения формы такой же, как у цилиндрических линз: преломление. Свет отклоняется в одном направлении или по одной оси, в то время как другая ось остается постоянной ( Рисунок 10 ). Это компенсирует разные углы расходимости луча.

Рис. 10: Анаморфотная пара призм, действующая как расширитель луча в одном направлении, которая может округлить эллиптический луч.

Одинокая призма может изменить радиус луча по одной оси, но это также изменит направление луча. Две призмы необходимы для сохранения исходного направления распространения луча при изменении его эллиптичности. Анаморфные пары призм сохраняют параллельность исходному направлению, но смещают луч в перпендикулярном направлении. Использование пар анаморфотных призм также требует точного углового выравнивания для правильной работы. Это не обязательно, но полезно, чтобы одна призма была ориентирована под углом Брюстера или углом падения, при котором p-поляризованный свет не отражается. Другая поверхность призмы будет находиться под прямым углом к лучу и должна быть покрыта просветляющим (AR) покрытием, чтобы максимизировать пропускную способность. Требуемая точная настройка приводит к тому, что многие интеграторы оптических систем покупают их в виде предварительно настроенной пары.

Высококачественные лазерные диоды часто имеют пары анаморфотных призм, встроенных в их лазерную головку, для округления лучей. Однако многие более дешевые диоды этого не делают. Стоимость покупки отдельной пары анаморфотных призм и менее дорогого диода без встроенной пары анаморфотных призм может быть меньше, чем у более дорогого диода.

Цилиндрические линзы имеют больше степеней свободы, чем пары установленных анаморфотных призм, что затрудняет их юстировку. Цилиндрические линзы могут наклоняться, что делает анаморфотные призмы более щадящими при попытках независимого выравнивания осей. Особое внимание следует также уделить фокусному расстоянию цилиндрических линз, чтобы они располагались на правильном расстоянии от лазерного диода для получения коллимированного круглого выходного луча. Установленные пары анаморфотных призм более удобны для пользователя. Они предварительно настроены на фиксированную степень расширения, что избавляет от необходимости устанавливать и собирать их самостоятельно, как это было бы с цилиндрическими линзами. Призмы имеют только одну ось, которая должна быть независимо выровнена, поскольку пользователь просто перемещает призму на пути луча. Это устраняет этап выравнивания, экономя время пользователя и избавляя его от возможного разочарования. Физическое расположение анаморфотных призм относительно положения падающего лазерного луча также менее чувствительно.

Однако дополнительные степени свободы, предлагаемые цилиндрическими линзами, обеспечивают большую гибкость, что может быть полезно при проведении исследований и создании прототипов. Цилиндрические линзы также могут обеспечить более высокую пропускную способность, чем пары анаморфотных призм, особенно когда линзы имеют просветляющее покрытие. Свету не нужно проходить через столько материала в цилиндрических линзах, сколько в парах анаморфотных призм, и p-поляризованный свет будет потерян, если анаморфотные призмы используются под углом Брюстера. Для получения дополнительной информации ознакомьтесь с нашими указаниями по применению пар анаморфных призм.

	Цилиндрические линзы	Пара анаморфотных призм
Смещение балки	Не смещен	Перемещенный
Степени свободы	Высокий	Низкий
Чувствительность выравнивания	Высокий	Низкий
Пропускная способность	Высокий	Средний
Стоимость	Низкий	Низкий
След	Маленький	Маленький

Таблица 2: Сравнение пар цилиндрических линз и анаморфотных призм для циркуляризации луча.

Ссылки:

Ф. М. Дики и С. К. Холсуэйд, Формирование лазерного луча: теория и методы, Марсель Деккер, Нью-Йорк (2000).
Ласкин, Александр и Вадим Ласкины. «Оптика формирования луча для отображения преломляющего поля: важные характеристики для правильного выбора». проц. ИКАЛЕО. Том. 2010. (2010).
Ф.М. Дики, С.К., Хоуэйд, Д.Л. Шили, Приложения для формирования лазерного луча, Тейлор и Фрэнсис, ISBN 0-8247-5941 (2005).
Дж. Дурнин: J. Opt. соц. Являюсь. А 4 (1987) 651.

Предыдущий раздел Следующий раздел

Дополнительные ресурсы

Зачем использовать лазерный луч с плоской вершиной?
Углубленный взгляд на Axicons
Формирование отражающего лазерного луча
Рекомендации по использованию цилиндрических линз
Пара анаморфотных призм
Режимы лазерного резонатора
Регулировочное крепление для формирователей луча AdlOptica
Выравнивание AdlOptica πShaper
Выравнивание AdlOptica Focal πShaper
Почему стоит выбрать ахроматический цилиндрический объектив?
Что такое цилиндрические линзы?
Лаборатория лазерной оптики Серия видеороликов

Был ли этот контент полезен для вас?

Спасибо за оценку этого контента!

Полукруглая криволинейная балка, открывающаяся с усилением из различных ламинатов – IJERT

Полукруглая изогнутая балка, открывающаяся с усилением из различных ламинатов

Athira Boselal1

1PG Scholar

Инженерный колледж Шри Будды 90 007

, Кластер Алапужа Патанамтхитта Технологического университета Абдула Калама APJ,

Арчана Сукумаран 2

Факультет гражданского строительства Инженерный колледж Шри Будды

, кластер Алапужа Патанамтитта Технологического университета Абдула Калама,

, Аятил, Элавумтхитта П. О., Патанамтхитта-689 62 Ayathil, Elavumthitta P.O, Pathanamthitta-68962

Реферат-Многослойные балки предлагают проектировщикам номер Это исследование посвящено изучению поведения и характеристик железобетонных полукруглых изогнутых балок с отверстиями. В ANSYS были испытаны четыре железобетонных полукруглых криволинейных балки с проемом типа круглого, прямоугольного. Переменными, рассматриваемыми в программе, являются усиление балки в области проема, усиление (ограничение) стеклопластиком, BFRP, CFRP, ламинатом. Балки испытывали на действие двух точечных нагрузок на верхнюю грань средних пролетов с тремя опорами на нижнюю грань концов и среднюю часть балок. Программное обеспечение ANSYS использовалось для анализа методом конечных элементов (FEM). В этой статье в качестве предварительного исследования изогнутая балка моделируется в программе ANSYS, и ее отклонение сравнивается с эталонным журналом. Программное обеспечение ANSYS проверяется путем проверки процентной ошибки в результатах.

Ключевые слова: Полукруглые балки, Проемы, Различные ламинаты, Конечные элементы

1.ВВЕДЕНИЕ

Многослойные балки представляют собой составные системы с высокими железобетонными горизонтально полукруглыми изогнутыми балками, которые используются во многих областях, например, при строительстве современных перекрестков, круглых резервуаров для воды, несущих кольцевых балок, круглых балконов и т. д. , При строительстве современных зданий сеть труб и воздуховодов необходима для размещения основных услуг, таких как водоснабжение, канализация, кондиционирование воздуха, электричество, телефонная и компьютерная сеть. Обычно эти трубы и воздуховоды размещают под софитом балки и из эстетических соображений накрывают подвесным потолком, создавая таким образом мертвое пространство. Проведение этих воздуховодов через поперечные отверстия в балках перекрытий уменьшит мертвое пространство и приведет к более компактной конструкции. Для небольших зданий экономия мертвых зон может быть незначительной,

, но для многоэтажных зданий любая экономия высоты этажа, умноженная на количество этажей, может означать существенную экономию общей высоты, длины воздуховодов и электрических каналов, сантехнических стояков, поверхностей стен и перегородок и общей нагрузки на фундамент. Горизонтально изогнутая кольцевая балка, нагруженная поперек своей плоскости, помимо изгиба и сдвига подвергается кручению. Кроме того, очевидно, что включение отверстий в балки меняет простое поведение балки на более сложное. Из-за резких изменений конфигурации сечения углы проема подвержены высокой концентрации напряжений, что может привести к недопустимому с точки зрения эстетики и долговечности растрескиванию. Уменьшенная жесткость балки также может привести к чрезмерному прогибу под рабочей нагрузкой и значительному перераспределению внутренних сил и моментов в сплошной балке. Если не обеспечить в достаточном количестве специальной арматуры с соответствующей деталировкой, прочность и работоспособность такой балки могут серьезно пострадать. На практике наиболее распространенными формами проемов являются круглая и прямоугольная.

Рис.1.1 Балкон с изогнутой балкой

Рис.1.2 Купол с изогнутой балкой

Области применения изогнутой балки

В этой главе описывается методология дипломной работы. Методология включает изучение изогнутой балки и программного обеспечения ANSYS. Вся дипломная работа делится на следующие последовательные этапы. Следующая блок-схема представляет методологию дипломной работы, которую необходимо выполнить.

Моделирование
Модели созданы с использованием программного обеспечения ANSYS. Затем необходимо проанализировать различные модели. Был проведен анализ. После анализа полученные результаты оцениваются, чтобы выяснить, какой тип проема в криволинейной балке лучше для различных конфигураций и наиболее эффективен в сопротивлении боковым нагрузкам. Обзор литературы помогает получить знания об изогнутой балке. Здесь необходимо провести исследование поведения изогнутой балки. Свойства материала выбираются на основе нескольких источников, таких как обзоры литературы. Материалы, используемые для CFRP, GFRP.BFRP,. изготовлены балочные образцы для анализа
Детали размеров
Изогнутая балка моделируется с помощью программного обеспечения ANSYS со справочным журналом[3]. Результаты конечно-элементного анализа были использованы для разработки статического анализа балок.:
Рис.3.1 Размеры сэндвич-балки
Свойства материалов
Изогнутая балка состоит из различных материалов. Свойства материала изогнутой балки приведены ниже
.
Таблица.3.2 Свойства материала GFRP
Таблица 3.3 Свойства материала CFRP
Таблица.3.4 Свойства материала BFRP
Рис.3.2 Окружное отверстие в балке
Рис.3.3 изогнутое отверстие в средней опоре
Рис.3.4.прямоугольное отверстие на средней опоре
Рис.3.5 прямоугольное отверстие
Создание сетки и загрузка
Балка моделируется с помощью прямоугольной сетки, состоящей из 4 узлов. Размер элемента сетки был предусмотрен 25мм. Загрузка предусмотрена на
верхняя площадь, как давление в 10кН. Нагрузка двухточечная.
Рис.3.6 Зацепление многослойной балки
Рис.3.7 Загрузка многослойной балки
Анализ изогнутой балки

Анализ выполнен с использованием программного обеспечения ANSYS. Анализ методом конечных элементов предоставит подробные сведения о поведении члена; он выполняется с правильными граничными условиями и свойствами материала. В этом исследовании проводятся различные анализы. К ним относятся эффекты собственных частот

, формы колебаний, вибрационные эффекты, демпфирующие эффекты в условиях точечной нагрузки.

Деформация

Рис. 3.8 Диаграмма деформации балки

Табл. 07

результаты сравнения. В ходе исследования были получены следующие выводы: круглое отверстие более эффективно, чем прямоугольное, в различных положениях, тогда внешняя упаковка углепластика дает лучший результат по сравнению с другими типами ламината по сравнению с прямоугольным и круглым отверстием.

ПОДТВЕРЖДЕНИЕ

Я благодарен моему проводнику, Асст. Профессору Арчане Сукумаран на факультете гражданского строительства за ее постоянную поддержку и умелое руководство. Также я благодарю своих родителей, друзей и т. д. за их постоянную поддержку в завершении этой работы

ССЫЛКИ

Д. С. Рамакришна и Ракшит Н., Простая механическая модель изогнутых балок с использованием трехмерного подхода, Международный журнал инженерных изобретений, том. 3(12), стр. 18-28, 2014.
Haider M. Alsaeq Влияние формы и расположения отверстий на структурную прочность железобетонных конструкций. круглые балки с открытием. (2013) Международный журнал машиностроения (IJME), IASET, ISSN(P): 2319-2240; ISSN(E): 2319-2259 Том. 3, выпуск 6, ноябрь 2014 г., стр. 37-44.
HM Alsaeq Вибрации в плоскости круговых изогнутых балок с открытием Journal of Construction Steel research, vol. 100, стр. 221-228, 2014.
Jithinbose KJ Влияние проемов в балках Обзор Исследовательский журнал прикладных наук, техники и технологий Vol. 4, № 9, стр. 1172-1180,2012
Киджун Кан и Дживон Хан Анализ изогнутой балки с использованием классической теории и теории деформируемой балки при сдвиге Структурный журнал ACI, том 109, 2012 г.
Мансур, Массачусетс Руководство по проектированию и строительству систем FRP с наружным приклеиванием для усиления бетонных конструкций Международный журнал научных и технологических исследований, том 3, 2014 г.