Откосы видео: Видео — Отделка откосов (видеоинструкция)

Утепление откосов (+ видео) — Утепление откосов (+ видео) — Готовые решения

Основываясь на опыте консультирования по вопросам теплоизоляции и разработке схем утепления для разнообразных зданий и сооружений, мы можем говорить о существовании часто встречаемой проблемы теплоизоляции зданий – о теплопотерях через оконные откосы.

Клиенты приходят к нам, недоумевая: поставили пластиковые окна, думали – станет теплее, а от окон по-прежнему холодно. После пары вопросов оказывается, что дует не от окна, а от оконного проёма, от откосов. Выпадает конденсат, люди живут с тряпками на подоконниках, на откосах и подоконнике распространяется плесень. В консультационный центр обращаются жители не только старого фонда, но и новых домов с вентилируемыми и утеплёнными фасадами.

Через старые окна с двойным остеклением происходили мощные теплопотери – и эта проблема решена стеклопакетами. Но есть одна деталь: толщина старого блока была в 3 – 3,5 раза больше, чем толщина стеклопакета. «Буферная зона» между улицей и помещением была шире. С установкой тонкого и энергоэффективного стеклопакета теплопотери начинают происходить через стыки оконного блока с материалом ограждающей конструкции (стены), потому что вокруг оконного блока возникают мостики холода – ведь линейное расстояние между помещением и улицей теперь стало меньше.

Рисунок 1. Влияние ширины оконного блока на теплопотери через откосы.

Проблема с холодными откосами в зданиях с утеплённым фасадом также имеет своё объяснение. При внешнем утеплении стен вся несущая стена здания (собственно ограждающая конструкция) в течение всего отопительного периода оказывается в зоне положительной температуры. При этом, если имеются хоть какие-то части ограждающей конструкции, выступающие из утепления (или недоутеплённые по сравнению с остальной стеной), то теплопотери через них будут значительно больше, чем до утепления. И именно откосы чаще всего оказываются этим «слабым звеном». Ведь фасадными системами утепляется только наружная плоскость стены, откос остаётся неутеплённым.

Рисунок 2. Схема теплопотерь через откосы при утеплённом фасаде. 1 – утепляемая стена 2 – утеплитель наружной фасадной системы 3 – оконная коробка 4 – стеклопакет 5 – тепловой поток по мостику холода 6 – неутеплённый оконный откос 7 – оконная рама из профилей ПВХ

После вычислений, проведённых нами совместно с Институтом Строительной физики (НИИСФ РААСН) выяснилось, что при учёте влияния неутеплённых откосов, утепление стен внешними фасадными системами не позволит достичь даже минимальных требуемых значений приведённого сопротивления теплопередачи по СНиП «Тепловая защита зданий» по Московской области.

Вопрос о том, какой тонкий и эффективный материал возможно применить для утепления откосов, неизбежно привёл нас к пенополиуретану (ППУ) – лучшему массивному изолятору на сегодняшний день, применяемому нами для производства строительной теплоизоляции.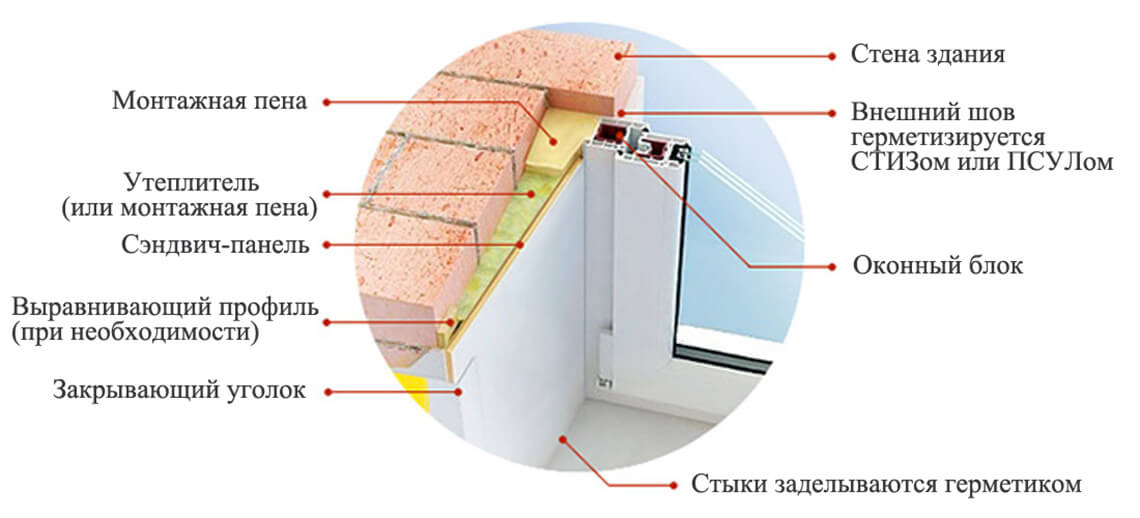 Полиуретан – двухкомпонентный пластик, который при плотности около 30-40 кг/м3 характеризуется самым низким коэффициентом теплопроводности среди современных утеплителей: λ=0,025 Вт/м*К.

Имея богатый опыт в изготовлении строительной изоляции из ППУ (более 12 лет) и понимая, какой плотности должен быть полиуретан для наилучшего утепления, мы разработали панели для одновременной отделки и утепления откосов. Толщина панели не превышает 10 миллиметров.

Способ монтажа – приклеивание на поверхность откоса ограждающей конструкции с помощью полиуретанового клея. Никаких специальных навыков для работы с полиуретаном не требуется. 

Мы рассчитали схемы утепления с определением точки росы для двух видов откосов (без внешнего утепления фасада и с внешним утеплением фасада). Как видно на рисунках и видео, применение пенополиуретана в откосах сокращает теплопотери и переносит точку росы.

Ниже приводятся схемы для наиболее распостранённого варианта оконного проёма — т. н. установки «в четверть«. В видеоролике в конце статьи приведено девять вариантов откосов с расчётами теплопотерь и точки росы.

Рисунок 3. Неутеплённый оконный откос: точка росы смещена внутрь помещения, выпадает конденсат.

 

Рисунок 4. Откос утеплён «Оконным откосом Регент». Точка росы уводится из помещения, конденсата нет, теплопотери резко сокращаются, повышается комфортность проживания.

Востребованность этой услуги (по нашему опыту теплотехнических консультаций) высока не только для жильцов старого фонда, но и для новостроек. Применение тёплых откосов в новых домах позволит пересмотреть общую схему утепления зданий и снизить затраты на общее утепление при гарантии уровня комфортности проживания и соответствия новым стандартам энергосбережения.

Посмотрите видео со схемами утеплённых и неутеплённых откосов и расчёты точки росы и выпадения конденсата:

Чем и как лучше покрасить откосы на окнах в помещениях с повышенной влажностью. + Видео

20 Февраль 2020

Основная функция откосов – барьерная. Они дополнительно защищают помещение от проникновения холодного воздуха, влаги и сырости снаружи.

Воздух в зоне оконного проема всегда более холодный и влажный, чем внутри помещения. И это все следует учитывать, выбирая лакокрасочные материалы для отделки откосов. Важно, чтобы конденсат, который всегда присутствует возле окна вследствие взаимодействия холодного и теплого воздуха, не разрушал гипсокартон и штукатурку.

Красить откосы нужно обязательно, это не только дополнительно защитит их от влаги, но и придаст длительный эстетический вид.  Правильно подобранная краска будет отталкивать влагу, пыль и грязь, предотвращать появление плесени.

Подготовка откоса

Заниматься откосами начинают уже после того, как смонтирован оконный профиль. Установлен и закреплен. Обязательно следует защитить окно от загрязнений – покрыть пленкой и заклеить малярным скотчем.

Предварительно откос очищают от старого покрытия, зашлифовывают поверхность. Затем шпаклюют.

Шпаклевка откоса

Шпаклевка для откоса наносят тонким слоем, не более 2 мм. Хорошо выравнивают все неровности. Дают просохнуть и зашлифовывают мелкозернистой наждачной бумагой. Проверяют поверхность с помощью дополнительного освещения (лампы). Акриловая шпаклевка Element выровняет поверхность, сделает ее равномерно гладкой и аккуратной. Она универсальна, поэтому подходит для внутренних и наружных работ.

Грунтовка откоса перед покраской

После полного высыхания, наносят грунтовку. Ее задача — глубоко проникнуть и сделать сцепление лакокрасочного материала с поверхностью более надежным. А также улучшить водоотталкивающие и поглощающие свойства штукатурки, бетона, кирпича, гипсокартона и других материалов, повысить адгезию краски. Грунтовка Element для оконных откосов наносится тщательно, поверхности дают хорошо высохнуть.

Выбор краски для откосов

Для откосов практически всегда выбирают краску белого цвета. Это может быть масляная эмаль или водно-дисперсная.

Важно учесть влажность помещения.  Помните, что масляная эмаль долго сохнет, имеет резкий запах, поэтому для жилых помещений ее не рекомендуется использовать.

Водно-дисперсная краска для влажных помещений – идеальный вариант. Она экологически чистая, без запаха, быстро сохнет. Обладает высокими влагоотталкивающими свойствами, защищает откосы от грибка, плесени, делает поверхность бархатистой, стойкой к механическим воздействиям. Компания Element рекомендует для таких работ краску для кухни и ванной комнаты.

Выбирая краску для откосов, не экономьте. Качественный вариант даст возможность надолго сохранить технические и эстетические свойства материала. Для удобства всегда можно подобрать оптимальный объем ЛКМ.

Покраска откоса

Не менее важно правильно подобрать инструмент для окрашивания откосов. Он должен быть надежным и качественным, не лезть. Неширокий валик, узкая кисть для труднодоступных мест – это, пожалуй, и все, что нужно на этом этапе.

Сначала прокрашивают углы, затем валиком аккуратно проходят по всей поверхности откоса. Движения равномерные и легкие, без натиска. Дабы избежать разводов и пятен, работают не отвлекаясь. Важно, чтобы краска легла ровным и гладким слоем.

Сразу рекомендуется снять малярный скотч и пленку, пока краска не присохнет.

Учитывайте все вышеизложенные рекомендации. Консультируйтесь со специалистами и правильно подбирайте краску для влажных помещений. Выполнив все рекомендации, можно быть твердо уверенным, что качество откосов не поменяется как минимум 5-6 лет.

Твитнуть

Поделиться

Поделиться

Отправить

Запинить

Видео-урок: Наклоны параллельных и перпендикулярных линий

Стенограмма видео

В этом видео мы рассмотрим работа с параллельными и перпендикулярными линиями. Мы пройдемся по определениям термины параллельно и перпендикулярно, а затем мы посмотрим на их уравнения и пойдем над некоторыми вопросами. Две прямые называются параллельными находятся ли они в одной плоскости, и независимо от того, насколько далеко вы их растянете в каждом направлении, они находятся на одинаковом расстоянии друг от друга. Другое популярное определение также говорит, что они никогда не должны пересекаться. И эффект от этого определения заключается в том, что если у вас есть две строки, которые на самом деле являются одной и той же строкой, по одной поверх каждой во-вторых, они не параллельны, потому что пересекаются в бесконечном числе различные места. Так что, хотя они всегда одинаковы расстояние друг от друга, ноль, мы не считаем их параллельными, потому что они пересекаются.

Вот пример, когда мы получил две разные строки. Они оба находятся на 𝑥𝑦-координате плоскость и они параллельны. Где бы вы ни измеряли расстояние между ними вы всегда получите один и тот же ответ. Говорят, что две строки перпендикулярны, если в точке их пересечения образуется прямой угол, как это здесь. Таким образом, эти две линии находятся на 𝑥𝑦-координатная плоскость и они пересекаются в точке два, ноль. И угол между ними есть 90 градусов. В остальной части этого видео мы будем работать только с линиями в 𝑥𝑦-координатной плоскости. А мы будем смотреть на уравнения этих линий, выбирая аспекты, которые говорят нам, параллельны они или они перпендикулярны.

И уравнения прямых действительно важная часть этой темы, так что давайте просто кратко повторим 𝑦 equals 𝑚𝑥 плюс 𝑏. Итак, общий вид уравнения прямой линии 𝑦 равно 𝑚𝑥 плюс 𝑏 или, может быть, 𝑦 равно 𝑚𝑥 плюс 𝑐, в зависимости от того, где вы живете. 𝑚-значение, кратное 𝑥, коэффициент 𝑥 говорит вам о наклоне линии. И значение 𝑏 говорит вам, где он пересекает ось 𝑦. Теперь наклон или градиент линия определяется как величина, на которую изменяется 𝑦-координата, когда мы увеличить 𝑥-координату на единицу.

Теперь я нарисовал две точки 𝑎 и 𝑏 на моей линии, и я увеличил 𝑥-координату на единицу, чтобы получить от 𝑎 до 𝑏. Так что разница в их 𝑥-координаты положительны. И когда я это делаю, разница в 𝑦-координатах от 𝑎 до 𝑏 будет увеличение на 𝑚. Итак, какое бы это значение ни было, хорошо, это величина, на которую увеличивается 𝑦-координата каждый раз, когда я увеличиваю свою 𝑥-координировать вверх на единицу, двигаясь вдоль линии. Итак, если бы эта строка была для пример 𝑦 равно 0,5 𝑥 плюс три, кратное 𝑥, наклон, значение 𝑚 равно 0,5. Это означает, что каждый раз, когда я увеличьте мою 𝑥-координату на единицу, моя 𝑦-координата увеличится на 0,5.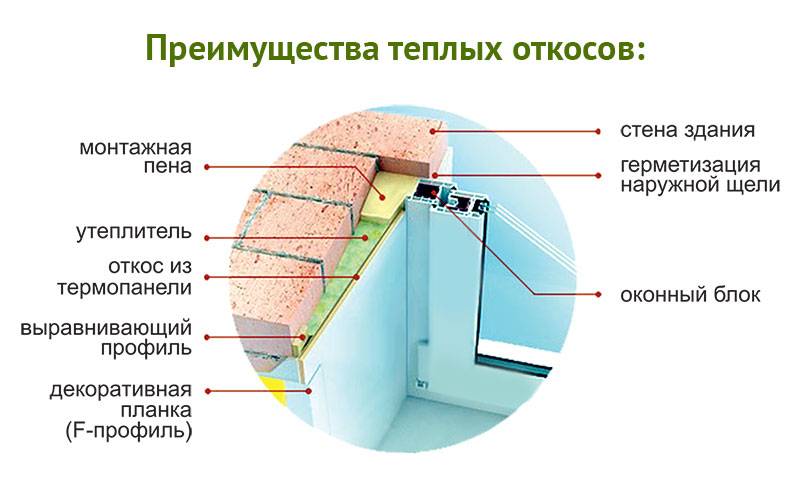

Итак, если составить уравнение строка в этом формате 𝑦 равна 𝑚𝑥 плюс 𝑏, то очень просто читать с наклона этой линии. Просто посмотрите на коэффициент 𝑥, кратное 𝑥; это ваш склон. Итак, у нас есть вопрос.

Какой из следующих прямых линии имеют одинаковый наклон или градиент? И тогда у нас есть пять линий. A равно 𝑦 равно трем 𝑥 минус Семь. B равно 𝑦 минус половина 𝑥 плюс три. C равно 𝑦 минус три 𝑥 плюс Семь. D равно 𝑦 минус половина 𝑥 плюс пять. И E равно 𝑦 равно трем 𝑥 плюс девять. Теперь все эти уравнения уже в формате 𝑦 равно 𝑚𝑥 плюс 𝑏 для нас, поэтому нам нужно посмотреть при 𝑥-коэффициентах. И если они одного номера с одинаковый знак, то они будут иметь одинаковый наклон или уклон.

Значит, B и D имеют одинаковый наклон, или градиент, отрицательная половина. А и Е имеют одинаковый наклон три. C имеет отрицательный наклон три, так что это другой знак, чем А и Е. Так что это не тот же наклон или градиент. Теперь, когда две строки имеют одинаковые наклон или градиент, мы называем их параллельными. Итак, здесь А параллелен Е и В параллелен D.

Итак, теперь мы можем распознать параллель линии, просто взглянув на их уравнения, если они находятся в 𝑦 равно 𝑚𝑥 плюс формат 𝑏. Итак, думая о наклоне перпендикулярные прямые, если две прямые перпендикулярны, то произведение их уклоны, или градиенты, являются отрицательными.

Ну, с чего бы это? Давайте взглянем. Итак, у меня здесь две строчки, 𝐿 одна, которому я дал уравнение 𝑦 равно 𝑚𝑥 плюс 𝑎, а 𝐿 два, которые я дал уравнение 𝑦 равно 𝑛𝑥 плюс 𝑏. Возьмем эту точку пересечение, а затем точка на каждой из этих прямых, имеющая 𝑥-координату что на единицу больше этой 𝑥-координаты в точке пересечения.

Для первой линии разница в 𝑦-координаты между этими двумя точками, этой и этой, будут 𝑚. А для второй строки разница в эти координаты будут 𝑛. Ну на самом деле так и будет отрицательный 𝑛. Итак, вторая линия — это нисходящая линия, что означает, что он будет иметь отрицательный градиент.

В данный момент меня интересует расстояние здесь. И это позитив расстояние. Так что мне нужно взять отрицательный этот отрицательный градиент, чтобы определить, каким будет это фактическое расстояние. Теперь, если я обозначу эти точки А, В, и C, мы знаем, что треугольник ABC прямоугольный, потому что две прямые перпендикулярны. Значит угол АВС прямой угол. А в прямоугольных треугольниках мы по теореме Пифагора можно сказать, что квадрат гипотенузы равен сумма квадратов других сторон.

Итак, квадрат длины AC равен длина AB в квадрате плюс длина BC в квадрате. И мы знаем, что длина AC равна 𝑚 плюс минус 𝑛. Итак, квадрат переменного тока равен 𝑚 плюс минус 𝑛 все в квадрате. Теперь, если мы вернемся к нашей диаграмме, мы видим, что у нас есть еще два прямоугольных треугольника. У нас есть вот это и это один здесь.

И снова мы можем использовать Теорема Пифагора для определения длины гипотенузы каждого из них. Мы знаем, что верхний треугольник имеет высота ℎ и ширина — извините, высота 𝑚 и ширина один. И нижний треугольник имеет высота отрицательного 𝑛 и ширина один. Таким образом, длины АВ и ВС равны квадратный корень из 𝑚 в квадрате плюс один в квадрате и квадратный корень из отрицательного 𝑛 всего в квадрате плюс один в квадрате. И теперь мы можем начать упрощать этот. 𝑚 плюс минус 𝑛 это просто 𝑚 взять далеко 𝑛.

Таким образом, левая часть становится 𝑚 минус 𝑛 все в квадрате. Квадратный корень из 𝑚 в квадрате плюс один в квадрате — это всего лишь 𝑚 в квадрате плюс один. А отрицательное 𝑛 все в квадрате просто 𝑛 в квадрате. Итак, квадратный корень из отрицательного 𝑛 все в квадрате плюс один в квадрате все в квадрате это просто 𝑛 в квадрате плюс один.

Теперь 𝑚 минус 𝑛 все в квадрате означает 𝑚 минус 𝑛 раз 𝑚 минус 𝑛 и просто приведя в порядок правую сторону, я получил 𝑚 в квадрате плюс 𝑛 ​​в квадрате плюс два. Теперь, умножая каждое слагаемое в первую скобку на каждый член во второй скобке с левой стороны, я получаю 𝑚 в квадрате минус два 𝑚𝑛 плюс 𝑛 ​​в квадрате. Так что я могу вычесть 𝑚 в квадрате из обе стороны, и я могу вычесть 𝑛 в квадрате с обеих сторон, что исключает 𝑚 в квадрате с обеих сторон и исключает 𝑛 в квадрате с обеих сторон.

Значит у меня минус два 𝑚𝑛 равно до двух. Теперь, если я разделю обе части на минус два, я получаю 𝑚 раз 𝑛 равно двум минус два, что равно отрицательный. Теперь помните, 𝑚 был наклоном моя первая линия, а 𝑛 был наклоном моей второй линии. Итак, 𝑚𝑛 — произведение двух наклоны линий. Итак, когда эти строки были перпендикулярно, неважно, каковы были фактические уклоны, мы знали, что, когда мы перемножив их вместе, мы всегда получим отрицательный ответ.

Теперь, если вы немного заблудились на во время этого объяснения, не волнуйтесь. Это не важно. Это то, что вы должны помнить. Если две прямые перпендикулярны, тогда произведение их наклонов или градиентов отрицательно. Итак, если мы назовем 𝑚 наклон первая строка и 𝑛 наклон второй строки, 𝑚 умноженный на 𝑛 равно отрицательному один. Или, если я разделю обе части на 𝑛, я получить 𝑚 равно минус единице сверх 𝑛. Или, если я разделю обе части на 𝑚, я получить 𝑛 равно минус один больше 𝑚. Другими словами, каждый наклон является отрицательное взаимное значение другого. Это означает, что если я знаю один из наклоны, я могу найти перпендикулярный наклон, просто изменив знак и перевернуть этот номер.

Например, если 𝑚 равно пяти, 𝑛 будет просто минус один больше пяти, противоположный знак, а затем перевернуть это число. Если 𝑚 было минус три, я беру противоположный знак, чтобы сделать его положительным и перевернуть это число, три на один становится одним более трех. А если бы 𝑚 было равно двум третям, 𝑛 будет отрицательным числом три больше двух. Таким образом, знание этого правила означает, что если вы знаете градиент или наклон определенной линии, с этим очень легко работать каков градиент или наклон перпендикулярной линии к этой линии. быть.

Подытоживая основные факты, два прямые параллельны, если они имеют одинаковый наклон, но разные 𝑦-пересечения. Например, 𝑦 равно семи 𝑥. минус пять и 𝑦 равно семи 𝑥 плюс два. Они оба имеют наклон семь и их 𝑦-перехваты различны, минус пять и плюс два, поэтому они параллельно. Две прямые перпендикулярны, если произведение их наклонов равно единице. Например, 𝑦 равно трем 𝑥 минус один и 𝑦 равно минус треть 𝑥 плюс девять. Наклон первой равен трем и наклон второго отрицателен в третьем. Таким образом, произведение этих наклонов равно трижды минус треть. Но три это то же самое, что и три один, поэтому, чтобы сделать это дробным расчетом, я получил три отрицательных значения один раз три. Ну, это минус три три, что равно отрицательной единице. Таким образом, он соответствует критериям, поэтому линии перпендикулярны.

И еще один пример, 𝑦 равно минус две седьмых 𝑥 плюс восемь и 𝑦 равно семи на два 𝑥 плюс восемь. Наклоны отрицательные в два раза семь и семь больше двух. Они являются отрицательной обратной величиной друг друга. И если я умножу наклоны вместе минус два больше семи умножить семь на два равно минус четырнадцать больше четырнадцати, что равно отрицательной единице. Итак, эти две строки перпендикуляр. А с перпендикулярными линиями это не имеет значения, что оба этих перехвата были на положительной восьмерке. Склоны разные, поэтому они это разные линии. Они определенно перпендикуляр. Давайте посмотрим на некоторые типичные тогда вопросы.

Две линии, A и B, имеют уклон три четверти и минус четыре больше трех соответственно. Они параллельны, перпендикулярны, или ни то ни другое?

Ну, наклоны не равны, так что они точно не параллельны. Теперь, если мы умножим эти наклоны вместе мы получаем три четверти, умноженные на четыре, умноженные на три, что отрицательно. двенадцать на двенадцать, что является минусом. Так что похоже, что эти два сл- линии будут перпендикулярны.

Следующая, какая из следующих строк параллельны друг другу? И тогда у нас есть пять уравнения. A) 𝑦 равно восьми 𝑥 минус пять. Б) Два 𝑦 равно восьми 𝑥 плюс три. C) Восемь 𝑥 минус 𝑦 плюс два равен нулю. D) Половина 𝑦 минус четыре 𝑥 равно двенадцать. И E) 𝑦 равно минус восьмая 𝑥 плюс семь.

Что ж, с А и Е они уже в формате 𝑦 равно 𝑚𝑥 плюс 𝑏, поэтому достаточно легко прочитать, какой наклон является. Но для B, C и D мы собираемся нужно немного переставить, чтобы получить их в правильном формате, чтобы иметь возможность читать с их склонов. Для уравнения B мне нужно разделите обе части этого уравнения на два. Итак, левая сторона, половина из двух 𝑦 это просто 𝑦. А затем разделив каждое слагаемое на справа на два, половина из восьми 𝑥 равна четырем 𝑥, а половина из трех равна трем больше два. Для уравнения C я могу просто добавить 𝑦 в обе стороны, что устранит его с левой стороны и даст мне просто 𝑦 с правой стороны. Так что это дает мне восемь 𝑥 плюс два равно 𝑦. Сейчас я просто напишу это наоборот, 𝑦 равно восьми 𝑥 плюс два, потому что это формат, в котором мы знаком с.

Теперь D нужно немного больше работа. У меня есть 𝑦 и 𝑥 срок на слева, а затем только число справа. Итак, прежде всего, я собираюсь добавить четыре 𝑥 в обе стороны, что дает мне половину 𝑦 равно, ну двенадцать плюс четыре 𝑥 или четыре 𝑥 плюс двенадцать. А затем удвоить каждую сторону этого уравнение, чтобы оставить мне только 𝑦. Два лота по половине 𝑦 равны 𝑦, два партии из четырех 𝑥 — это восемь 𝑥, а две партии из двенадцати — это двадцать четыре. Теперь у нас есть наши уравнения в правильный формат. Это довольно просто дело в нахождении наклонов, чтобы мы могли видеть, какие прямые параллельны каждому другой. В A наклон равен восьми. В B наклон равен четырем. В C наклон равен восьми. В D наклон также равен восьми. А в E наклон отрицательный восьмой. Таким образом, A, C и D имеют наклон восемь. Таким образом, ответ A, C и D равны параллельно.

Теперь мы должны написать уравнение прямой, параллельной 𝑦, равно восьми 𝑥 минус четыре.

Значит, это должно быть параллельно, что означает, что он должен иметь тот же наклон, равный восьми. Итак, нужно начать с 𝑦 равно восьми 𝑥. И тогда мы можем добавить все, что мы например, потому что везде, где эта линия пересекает ось 𝑦, это не имеет значения. Это будет параллельно линия. Единственное, что вы не должны использование восемь 𝑥 минус четыре. Не делайте это точно такой же линией потому что большинство людей сказали бы, что они не параллельны, потому что это одно и то же линия. Так что можешь писать что хочешь здесь восемь 𝑥 плюс тысяча. Здесь мы идем, это линия, которая параллельно 𝑦 равно восьми 𝑥 минус четыре.

Далее мы должны написать уравнение прямой, перпендикулярной 𝑦, равно трем 𝑥 минус два.

Ну, наклон три, значит наклон этой перпендикулярной линии должен быть отрицательным обратным, так что это минус один больше трех. Итак, наше уравнение начнется 𝑦 равно минус один больше трех 𝑥. И мы можем добавить все, что мы нравиться. Мы могли бы просто оставить это как минус один более трех 𝑥, или мы можем добавить любое число, которое нам нравится, чтобы сделать перпендикулярную линию.

Теперь нам нужно написать уравнение ибо прямая, параллельная 𝑦, равна половине 𝑥 плюс пять и проходит через точку шесть, 10. Ну, мы знаем, что наклон линия 𝑦 равна половине 𝑥 плюс пять имеет наклон, равный половине. Итак, если наша линия будет параллельной к этому он также должен иметь наклон в половину. Но, конечно, эта линия может сократить ось 𝑦 в любом месте, чтобы мы могли перемещать эту линию вверх или вниз. Нам говорят, что он должен пройти через точку шесть, 10. А это значит, что когда 𝑥 равно шести, 𝑦 должно быть 10.

Теперь, если мы используем общую форму наше уравнение 𝑦 равно 𝑚𝑥 плюс 𝑏, мы знаем, что наклон 𝑚 равен половине. Теперь нам предстоит выяснить, значение 𝑏. Но мы знаем конкретную координату пара, которая находится на линии, когда 𝑥 равно шести, 𝑦 равно 10. Таким образом, заменив 𝑥 и 𝑦 на шесть и 10, у нас 10 равно половине, умноженной на шесть, плюс 𝑏. Итак, 10 равно трем плюс 𝑏. А затем вычитая три из обе стороны, дает мне семь равно 𝑏. Теперь мы знаем значение 𝑏; мы можно закончить наше уравнение. 𝑦 равно половине 𝑥 плюс Семь.

Наконец, напишите уравнение для прямая, перпендикулярная 𝑦, равна трем четвертям 𝑥 минус четыре и проходит через точку четыре, 11.

Итак, мы пытаемся найти градиент, или наклон, перпендикулярный на три четверти. Значит наклон нашего перпендикуляра линия будет отрицательная четыре на три, отрицательная обратная, помните. Три четверти минус четыре больше трех равно отрицательной единице. значит это перпендикуляр линия. Итак, у нас есть наклон линии и мы также знаем, что он пройдет через точку четыре, 11. Итак, когда 𝑥 равно четырем, тогда 𝑦 равно 11. Таким образом, используя формат уравнения 𝑦 равно 𝑚𝑥 плюс 𝑏, мы знаем, что 𝑚 минус четыре плюс три. И мы знаем, что когда 𝑥 равно четырем, тогда 𝑦 равно 11. Таким образом, мы можем использовать всю эту информацию вычислить значение 𝑏.

Таким образом, 11 равно отрицательному значению четыре трети умножить на четыре плюс 𝑏. Ну, четыре это то же самое, что и четыре один. Так что это становится дробью расчет минус четыре трети, умноженные на четыре на один. Итак, 11 равно отрицательному шестнадцать третей плюс 𝑏. Итак, если я добавлю шестнадцать третей к обоим сторон, у меня 11 плюс шестнадцать третей равно 𝑏. И это равно 49 больше три. Так что я могу положить это обратно в наш исходное уравнение и получить мой ответ, 𝑦 равно отрицательным четырем третям 𝑥 плюс 49над три.

Интеграция видеонаблюдения по всему миру

Silicon Slopes Podcast: Интеграция видеонаблюдения по всему миру

Silicon Slopes · Интеграция видеонаблюдения по всему миру

Брент Эдмундс — генеральный директор Stone Security — коммерческой компании по интеграции систем безопасности, которая специализируется на системах видеонаблюдения и контроля доступа по картам. Stone Security сосредоточилась на создании прочных и лояльных партнерских отношений со своими клиентами с момента своего основания в 2005 году, и каждый сотрудник научился быть технологически подкованным, поскольку вся их работа основана на IP. Послушайте, чтобы узнать, как Stone Security и ее офисы в Солт-Лейк-Сити, Денвере и Вегасе помогают компаниям в разных странах мира.

Более новая статья

Zonos привлекает 69 миллионов долларов серии A

15 сентября 2021 г. 1 мин чтения

Старая статья

InMoment приобретает Lexalytics

14 сентября 2021 г. 1 мин чтения

Будьте в курсе! Получайте все последние публикации прямо в свой почтовый ящик.

Имя Электронная почта

Отлично! Проверьте свой почтовый ящик и нажмите на ссылку, чтобы подтвердить подписку.