Как будет вертикально и горизонтально: Горизонтали, вертикали и диагонали / Статьи / Newslab.Ru

Вертикально: это как – вверх или вниз и как выглядит вертикальная линия

Казалось бы, что каждому человеку должно быть известно, что обозначают такие термины как «вертикально», «горизонтально». Однако даже взрослые люди зачастую путаются это вверх или нет. В данной статье мы попробуем разобраться, какое положение считается вертикальным, как и где принято использовать это обозначение. Более того, мы поговорим и о том, какое значение отводится обычной вертикальной черте в некоторых школьных науках.

Содержание

Таблица ASCII и вертикаль

Сперва поговорим о том, что же должен представлять человек, когда слышит определение «вертикальная черта». В первую очередь, это обозначение используется именно в ASCII. Вам ничего не говорит данная аббревиатура? И это вполне нормально, поскольку данная шифровка будет знакома исключительно людям, работа которых связана с кодированным текстом.

Это интересно! Считаем правильно: как находить процент от суммы и числа

Для простых обывателей поясним, что ASCII представляет собой достаточно большую таблицу. В ней собраны различные коды. Каждый из этих кодов соответствует печатным и непечатным символам, которые широко используются.

Таблица ASCII

Обратите внимание! Речь идет именно о числовых кодах. Впервые эта таблица была разработана специалистами из Соединенных Штатов Америки в 60-х годах. Практически сразу после разработки она была стандартизирована и после этого начала активно использоваться.

В таблице можно найти и такой символ, как вертикальная линия. Ее код – 0x7C (hex), 124 (dec).

Примечательно, что пользователи операционной системы под названием UNIX, предпочитают именовать данный символ не иначе как «пайп». С английского языка слово «pipeline» можно перевести как конвейер. Но в Советском Союзе понять и принять данную терминологию не смогли. Книги В. Э. Фигурнова, первые издания которых являются советскими, пестрели необычным сравнением вертикальной линии с трубопроводом. Именно поэтому ее и начали именовать как символ трубопровода, заменив тем самым ходовое наименование «pipe».

Это интересно! Как найти и чему будет равна длина окружности

Применение в математике

Наверняка, каждый школьник, который не прогуливал уроки и добросовестно выполнял домашние задания, известно, как выглядит вертикаль. Ведь в математике обозначение используется довольно часто. Причем вариантов применения имеется немало.

Рассмотрим более подробно каждый из них и тем самым немного вспомним школьную программу.

1. |x| знакомое многим обозначение. Значение, которое находится между двумя вертикальными чертами, это абсолютное значение. Тоже никогда не слышали? Тогда напомним о другом термине, которым принято обозначать абсолютное значение. И это – модуль. Следовательно, линия, идущая вниз, обозначает именно модуль.
2. m || n – разделение двумя вертикальными чертами принято считать обозначением параллели. Иными словами, данные прямые (плоскости) всегда будут параллельными, если их разделяет подобный символ.
3. a|b – в такой формуле вертикальная линия представляет собой разделитель. То есть число a делит число b.
4. p(b|a) – более сложная формула. Разделение в виде вертикальной черты говорит о том, что некое событие b возможно только при условии, что произойдет событие a.

Вышеперечисленные формулы и обозначения не являются единственными. В математике достаточно много и других примеров использования вертикальной черты. Стоит упомянуть и о том, что она часто используется в другой науке, которую тоже преподают в школе.

Полезное видео: вертикальная черта

Специалисты, которые работают с такими системами как DOS и UNIX, знают, что такое вертикальная линия, поскольку часто с ней работают. Подобное объясняется тем, что именно это обозначение используется для Stdout. А что же представляет собой Stdout? Все просто – это процесс, который обозначает перенаправление стандартного потока вывода определенной программы в другой конвейер. bad | sort. Но сразу отметим, что она сложная только на первый взгляд. В действительности программист задал простой алгоритм. С его помощью можно вывести на экран список фруктов, который содержится в файле под названием fruits.txt.

Это интересно! Изучаем символы: как обозначается в математике площадь

Но при этом можно будет увидеть только те фрукты, в названии которых в первых 3-х символах нет «bad». Более того, выведенный список будет сразу отсортирован по алфавиту. Все просто, не так ли? Но какая же формула натолкнула программистов на мысль сравнить вертикаль с трубопроводом?

Та, что приведена выше. На примере этой формулы можно понять, почему же российским программистам пришло в голову сравнить данный символ с трубопроводом. Описанный метод передачи информации направляет поток данных по тому же принципу работы, что и обычный трубопровод. Именно поэтому программисты из Советского Союза посчитали, что термин «pipe», пришедший с Запада, можно заменить на другой «трубопровод». Ведь по вертикали это значит и вниз, и вниз.

Пример программы в информатике с использованием вертикальных линий

Просто о сложном

Практически у каждого человека, который прочитал вышеизложенный текст, гарантированно возникла мысль, что разобраться в том,какая линия вертикальна, сложно. Но в действительности это не так. Итак, сейчас попробуем простым и понятным языком объяснить, что же представляет собой вертикаль.

Это интересно! Урок геометрии: как найти по формуле периметр треугольника

Вертикаль – это направление, которое перпендикулярно горизонтальной плоскости. А теперь вспомним, что такое горизонтальная плоскость. Представьте себе горизонт. Представили? Вот вам и горизонтальная плоскость. Следовательно, плоскость, которая будет располагаться по отношению к горизонту перпендикулярно, должна считаться вертикальной чертой. То есть вертикально, как уже было написано, это вверх и вниз одновременно.

Полезное видео: Рисуем прямые линии (вертикальные и горизонтальные)

Горизонтальный или вертикальный кадр. Цифровая фотография от А до Я [2-е издание]

Горизонтальный или вертикальный кадр. Цифровая фотография от А до Я [2-е издание]

ВикиЧтение

Цифровая фотография от А до Я [2-е издание]
Газаров Артур Юрьевич

Содержание

Горизонтальный или вертикальный кадр

Правильно расположите камеру. Если вы снимаете вертикальный объект (человека во весь рост, высокое дерево, столб, башню и другие вытянутые вертикально объекты), стоит развернуть камеру и снять кадр вертикально. Если композиция вытянута вдоль линии горизонта (пейзаж, групповой портрет, лежащая на диване кошка и т. д.), кадр должен быть горизонтальным (рис. 6.1 и 6.2).

^{Рис. 6.1. Горизонтальное расположение объекта в кадре}

^{Рис. 6.2. Вертикальное расположение объекта в кадре}

Иногда, чтобы подчеркнуть особенность сцены, можно нарушить правила.

Когда вы хотите акцентировать взгляд зрителя на какой-то части объекта, можно передать его не полностью — на снятой части и будет сосредоточено внимание зрителей. Эта часть будет более динамично взаимодействовать в кадре с другими объектами. Не всегда удастся передать образ, сняв, например, человека во весь рост. Возможно, следует нарушить правила и оставить на снимке только ноги. Но зато они будут намного выразительнее и больше расскажут зрителю об отношении объекта с окружающим миром.

Стоит отметить, что иногда оптимальным выбором становится не горизонтальный и не вертикальный кадр. Оба будут смотреться менее выигрышно, чем золотая середина между ними — наклонный или диагональный кадр. Поэтому в некоторых случаях стоит камеру наклонить так, чтобы вытянутый объект в кадре образовывал диагональ (рис. 6.3).

^{Рис. 6.3. Диагональное расположение объекта в кадре}

Определив положение камеры при съемке, не стоит торопиться с нажатием кнопки спуска.

До этого предстоит продумать и выполнить некоторые действия, рассмотренные ниже.

Данный текст является ознакомительным фрагментом.

gotoAndPlay — Переход на кадр и воспроизведение

gotoAndPlay — Переход на кадр и воспроизведение gotoAndPlay(Глобальная функция)Осуществляет немедленный безусловный переход на указанный кадр, а затем воспроизводит текущий клип или фильм.Синтаксис:gotoAndPlay(frameNumber)gotoAndPlay(frameLabel)gotoAndPlay(scene, frameNumber)gotoAndPlay(scene,

gotoAndStop — Переход на кадр и остановка

gotoAndStop — Переход на кадр и остановка gotoAndStop(Глобальная функция)Осуществляет немедленный безусловный переход на указанный кадр, а затем останавливает текущий клип или фильм.

Синтаксис:gotoAndStop(frameNumber)gotoAndStop(frameLabel)gotoAndStop(scene, frameNumber)gotoAndStop(scene, frameLabel)Аргументы:Описание:Если

nextFrame — Переход на следующий кадр

nextFrame — Переход на следующий кадр nextFrame(Глобальная функция)Перемещает воспроизводящую головку текущего клипа или фильма на один кадр вперед и останавливает ее.Синтаксис:nextFrame()Описание:Функция nextFrame() перемещает воспроизводящую головку текущей временной диаграммы на

prevFrame — Переход на предыдущий кадр

prevFrame — Переход на предыдущий кадр prevFrameПеремещает воспроизводящую головку текущего клипа или фильма на один кадр назад и останавливает ееСинтаксис:prevFrame()Описание:Функция prevFrame() перемещает воспроизводящую головку текущей временной диаграммы на один кадр назад и

ifFrameLoaded — Выполняет код если загруженн определенный кадр

ifFrameLoaded — Выполняет код если загруженн определенный кадр ifFrameLoaded(Предложение)Выполняет некоторый код, если загружен определенный кадрСинтаксис:ifFrameLoaded(scene, frame) { statement;}ifFrameLoaded(frame) { statement;}Аргументы:Описание:Проверяет, доступно ли содержимое указанного кадра локально

Глава 2 Вертикальный поиск

Глава 2 Вертикальный поиск Важным направлением развития современного интернет-поиска стало появление большого количества специализированных поисковиков, предназначенных для углубленного поиска определенного тематического контента. Такие интернет-машины часто

Стоп-кадр

Стоп-кадр Конечно, можно использовать аватары, предлагаемые программой Skype в качестве изображений, которые будут видеть другие люди, но можно сфотографировать самого себя, то есть создать стоп-кадр и поместить его в качестве аватара.Фотографирование самого себяЧтобы

Компонуем кадр

Компонуем кадр Пейзаж – это всегда перспектива, а усилить впечатление от перспективы поможет формат снимка: горизонтальный или вертикальный. Большинство ландшафтов лучше смотрятся на снимке горизонтального формата, но порой бывает предпочтительнее вертикаль, которая

НАУКА: Заразные гены, или Горизонтальный поворот: Днк можно получить не только от родителей

НАУКА: Заразные гены, или Горизонтальный поворот: Днк можно получить не только от родителей Автор: Дмитрий ШабановЖурнал «Nature» публикует не только статьи о состоявшихся достижениях, но и эссе, авторы которых пытаются нащупать дальнейшие пути развития науки.

Одно из

Не переэкспонируйте кадр

Не переэкспонируйте кадр Лучше недодержать снимок — пересвеченный кадр уже не исправить, а недоэкспонированный достаточно неплохо «вытягивается» в редакторе. Если вы снимаете на открытом пространстве, где нет резких теней, установите матричный (оценочный) экспозамер.

Глава 6 Как правильно скомпоновать кадр

Глава 6 Как правильно скомпоновать кадр • Основные правила композиции• Горизонтальный или вертикальный кадр• Объект съемки не должен быть слишком мелким• Убираем все лишнее• Максимально заполняйте кадр• Правило трех третей• Фон• Правило левой руки• Линии в

Горизонтальный или вертикальный кадр

Горизонтальный или вертикальный кадр Правильно расположите камеру. Если вы снимаете вертикальный объект (человека во весь рост, высокое дерево, столб, башню и другие вытянутые вертикально объекты), стоит развернуть камеру и снять кадр вертикально. Если композиция

Максимально заполняйте кадр

Максимально заполняйте кадр «Природа не терпит пустоты» — эта фраза применима и к фотографии. Ничем не заполненное поле кадра смотрится не очень привлекательно. Когда большую часть кадра занимает, например, однотонное безоблачное небо или море, это оправдано, если

Как компоновать кадр при предметной съемке

Как компоновать кадр при предметной съемке Вовсе не обязательно снимать предметы прямо «в лоб». Такое расположение на снимке часто выглядит скучно и неинтересно. Попробуйте подойти к съемке творчески, поэкспериментируйте с ракурсами, сделайте несколько разных

Как построить кадр

Как построить кадр Натюрморт отличается от предметной съемки тем, что в нем предметы взаимодействуют друг с другом. Однако можно снять и натюрморт, в котором всего один объект. Главное — замысел, идея.В кадре должен быть один-единственный сюжетный центр. Когда их два и

Нечеткий кадр

Нечеткий кадр Нередко, несмотря на усилия, немалая часть снимков оказывается смазанной. Хотя вы считаете, что держите камеру неподвижно, это не так: руки человека всегда чуточку дрожат, хоть внешне это незаметно.Если вы сделали кадр в автоматическом режиме и он получился

3.2 Графические функции с использованием вертикальных и горизонтальных сдвигов – Math 3080 Подготовка

Часто, когда нам дают задачу, мы пытаемся смоделировать сценарий, используя математику в виде слов, таблиц, графиков и уравнений. Один из методов, который мы можем использовать, — это адаптировать базовые графики функций инструментария для построения новых моделей для заданного сценария. Существуют систематические способы изменения функций для построения подходящих моделей для проблем, которые мы пытаемся решить.

Определение вертикального смещения

Один из простых видов преобразования включает сдвиг всего графика функции вверх, вниз, вправо или влево. Самый простой сдвиг — это сдвиг по вертикали на , перемещающий график вверх или вниз, потому что это преобразование включает добавление к функции положительной или отрицательной константы. Другими словами, мы добавляем одну и ту же константу к выходному значению функции независимо от входных данных. Для функции [латекс]\текст{}g\left(x\right)=f\left(x\right)+k,\text{}[/latex] функция [латекс]\текст{}f\left (x\right)\text{}[/latex] смещается по вертикали на [latex]\text{}k\text{}[/latex] единиц. См. пример на Рисунке 3-2.

 

Рисунок 3-2: Вертикальный сдвиг на [latex]\text{}k=1\text{}[/latex] функции кубического корня [latex]\text{}f\left(x\right)=\sqrt[ 3]{x}[/латекс].

Чтобы помочь вам визуализировать концепцию вертикального сдвига, учтите, что [латекс]\текст{}у=f\влево(х\вправо)\текст{}[/латекс]. Следовательно, [латекс]\текст{}f\left(x\right)+k\text{}[/latex] эквивалентен [latex]\text{}y+k\text{}[/latex]. Каждая единица [латекс]\текст{}у\текст{}[/латекс] заменяется на [латекс]\текст{}у+к,\текст{}[/латекс], поэтому [латекс]\текст{} Значение y\text{-}[/latex] увеличивается или уменьшается в зависимости от значения [latex]\text{}k\text{}[/latex]. Результатом является сдвиг вверх или вниз.

Сдвиг по вертикали

Дана функция [латекс]f\влево(х\вправо)[/латекс], новая функция [латекс]г\влево(х\вправо)=f\влево(х\вправо)+ k[/latex], где [latex]\text{}k[/latex] — константа, — вертикальный сдвиг функции [latex]f\left(x\right)[/latex]. Все выходные значения изменяются на [latex]k[/latex] единиц. Если [latex]k[/latex] положителен, график сдвинется вверх. Если [latex]k[/latex] отрицательно, график сдвинется вниз.

Для регулирования температуры в зеленом здании вентиляционные отверстия возле крыши открываются и закрываются в течение дня. На рис. 3-3 показана площадь открытых вентиляционных отверстий [latex]\text{}V\text{}[/latex] (в квадратных футах) в течение дня в часы после полуночи, [latex]\text{}t\text{ }[/латекс]. Летом управляющий хозяйством решает попытаться лучше регулировать температуру, увеличив количество открытых вентиляционных отверстий на 20 квадратных футов в течение дня и ночи. Нарисуйте график этой новой функции.

Рисунок 3-3

Решение

Учитывая табличную функцию, создайте новую строку для представления вертикального смещения.

1. Укажите выходную строку или столбец.
2. Определите величину сдвига.
3. Добавьте сдвиг к значению в каждой выходной ячейке. Добавьте положительное значение вверх или отрицательное значение вниз.

Функция [latex]\text{}f\left(x\right)\text{}[/latex] указана в таблице 1. Создайте таблицу для функции [latex]\text{}g\left(x \right)=f\left(x\right)-3[/латекс].

Таблица 1

[латекс]x[/латекс]	2	4	6	8
[латекс]f\влево(х\вправо)[/латекс]	1	3	7	11

Анализ

Как и в случае с предыдущим сдвигом по вертикали, обратите внимание, что входные значения остаются прежними, а изменяются только выходные значения. 9{2}+30t\text{}[/latex] дает высоту [latex]\text{}h\text{}[/latex] мяча (в метрах), брошенного вверх с земли после [latex]\text {}t\text{}[/latex] секунд. Предположим, что вместо этого мяч был брошен с крыши 10-метрового здания. Свяжите эту новую функцию высоты [латекс]\текст{}b\left(t\right)\text{}[/latex] с [латекс]\text{}h\left(t\right)\text{}[/ латекс], а затем найдите формулу для [латекс]\текст{}b\left(t\right)[/латекс].

Раствор

Идентификация горизонтальных сдвигов

Мы только что видели, что вертикальный сдвиг — это изменение выхода или вне функции. Теперь мы посмотрим, как изменения ввода внутри функции изменяют ее график и значение. Сдвиг на входе приводит к перемещению графика функции влево или вправо в так называемом горизонтальном сдвиге , показанном на рисунке 3-4.

Рисунок 3-4: Горизонтальный сдвиг функции [латекс]\текст{}f\влево(х\вправо)=\sqrt[3]{х}\текст{}[/латекс]. Обратите внимание, что [latex]\text{}h=+1\text{}[/latex] сдвигает график влево, то есть в сторону отрицательных значений [latex]\text{}x[/latex].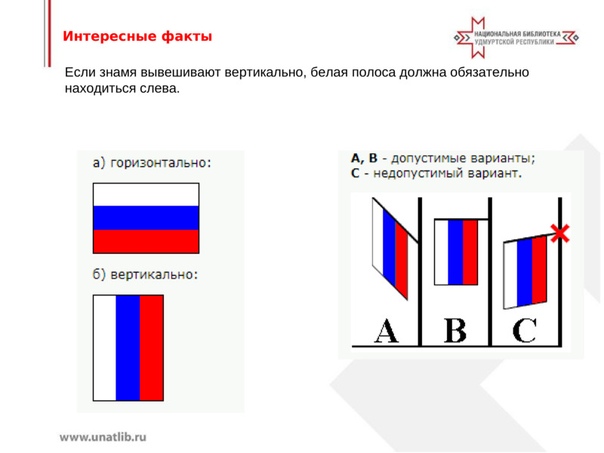 9{2}\text{}[/latex] – это новая функция. Каждый вход уменьшается на 2 перед возведением функции в квадрат. В результате график смещается на 2 единицы вправо, потому что нам нужно было бы увеличить предыдущий ввод на 2 единицы, чтобы получить такое же выходное значение, как указано в [latex]\text{}f[/latex].

Горизонтальное смещение

Учитывая функцию [латекс]\текст{}f\текст{}[/латекс], новую функцию [латекс]\текст{}г\влево(х\вправо)=f\влево( x-h\right)\text{}[/latex], где [latex]\text{}h\text{}[/latex] — константа, — сдвиг по горизонтали функции [latex]\text{}f\ текст{}[/латекс]. Если [latex]\text{}h\text{}[/latex] положительный, график сдвинется вправо. Если [latex]\text{}h\text{}[/latex] отрицательно, график сдвинется влево.

Возвращаясь к нашему примеру потока воздуха в здании из Примера 1 (Рисунок 3-5 ниже), предположим, что осенью руководитель предприятия решает, что первоначальный план вентиляции начинается слишком поздно, и хочет начать всю программу вентиляции на 2 часа раньше.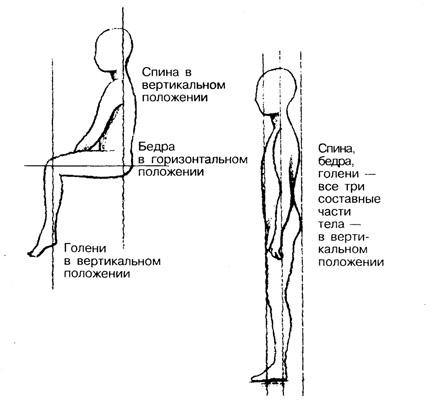 Нарисуйте график новой функции.

Рисунок 3-5 Анализ

Обратите внимание, что [latex]\text{}V\left(t+2\right)\text{}[/latex] приводит к смещению графика влево .

Горизонтальные изменения или «внутренние изменения» влияют на домен функции (вход), а не на диапазон, и часто кажутся нелогичными. Новая функция [latex]\text{}F\left(t\right)\text{}[/latex] использует те же выходные данные, что и [latex]\text{}V\left(t\right)\text{} [/latex], но сопоставляет эти выходные данные с входными на 2 часа раньше, чем [latex]\text{}V\left(t\right)\text{}[/latex]. Другими словами, мы должны добавить 2 часа к входным данным [latex]\text{}V\text{}[/latex], чтобы найти соответствующий вывод для [latex]F:F\left(t\right)=V \влево(т+2\вправо)[/латекс].

Решение

Учитывая табличную функцию, создайте новую строку для представления смещения по горизонтали.

1. Определите входную строку или столбец.
2. Определите величину сдвига.
3. Добавьте сдвиг к значению в каждой входной ячейке.

Функция [latex]\text{}f\left(x\right)\text{}[/latex] указана в таблице 2. Создайте таблицу для функции [latex]\text{}g\left(x \right)=f\left(x-3\right)[/латекс].

Таблица 2

[латекс]x[/латекс]	2	4	6	8
[латекс]f\влево(х\вправо)[/латекс]	1	3	7	11

Анализ

На рис. {2}\text{}[/latex]. Свяжите эту новую функцию [латекс]\текст{}г\влево(х\вправо)\текст{}[/латекс] с [латекс]\текст{}f\влево(х\вправо)\текст{}[/латекс ], а затем найдите формулу для [латекс]\текст{}г\влево(х\вправо)[/латекс].

Рисунок 3-7 Анализ

Чтобы определить, является ли сдвиг [латекс]\текст{}+2\текст{}[/латекс] или [латекс]\текст{}-2[/латекс], рассмотрим одиночный точка отсчета на графике. Для квадратичного удобно смотреть на точку вершины. В исходной функции [латекс]\текст{}f\влево(0\вправо)=0\текст{}[/латекс]. В нашей сдвинутой функции [латекс]\текст{}г\влево(2\вправо)=0\текст{}[/латекс]. Чтобы получить выходное значение 0 из функции [latex]\text{}f\text{}[/latex], нам нужно решить, какой знак плюс или минус будет работать для удовлетворения [latex]\text{}g \left(2\right)=f\left(x-2\right)=f\left(0\right)=0\text{}[/latex]. Для этого нам понадобится вычесть 2 единицы из наших входных значений.

Раствор

1. Функция [латекс]\текст{}Г\влево(м\вправо)\текст{}[/латекс] дает количество галлонов газа, необходимое для привода [латекс]\текст{}м\текст{}[ /латекс] миль. Интерпретировать [латекс]\текст{}G\влево(м\вправо)+10\текст{}[/латекс] и [латекс]\текст{}G\влево(м+10\вправо)[/латекс].
2. Учитывая функцию [латекс]\текст{}f\left(x\right)=\sqrt{x}\text{}[/latex], постройте график исходной функции [латекс]\текст{}f\left(x \right)\text{}[/latex] и преобразование [latex]\text{}g\left(x\right)=f\left(x+2\right)\text{}[/latex] на одинаковые оси. Это сдвиг по горизонтали или по вертикали? В какую сторону сместился график и на сколько единиц?

Раствор

Комбинация вертикальных и горизонтальных сдвигов

Теперь, когда у нас есть два преобразования, мы можем объединить их вместе. Вертикальные сдвиги — это внешние изменения, которые влияют на выходные значения оси [latex](y\text{-})[/latex] и сдвигают функцию вверх или вниз. Горизонтальные сдвиги — это внутренние изменения, которые влияют на входные значения оси [latex](x\text{-})[/latex] и сдвигают функцию влево или вправо. Сочетание двух типов сдвигов приведет к смещению графика функции вверх или вниз 9. 0181 и вправо или влево.

Учитывая функцию и вертикальное и горизонтальное смещение, нарисуйте график.

1. Определите вертикальное и горизонтальное смещение по формуле.
2. Сдвиг по вертикали является результатом добавления константы к выходным данным. Переместите график вверх для положительной константы и вниз для отрицательной константы.
3. Горизонтальное смещение является результатом добавления константы к входным данным. Переместите график влево для положительной константы и вправо для отрицательной константы.
4. Применить сдвиги к графику в любом порядке.

1. Учитывая [латекс]\текст{}f\left(x\right)=|x|\text{}[/latex], нарисуйте график [латекс]\text{}h\left(x\right) =f\влево(x+1\вправо)-3[/латекс].
2. Учитывая [латекс]\текст{}f\left(x\right)=|x|\text{}[/latex], нарисуйте график [латекс]\text{}h\left(x\right)= f\влево(x-2\вправо)+4[/латекс].

Раствор

1.  Напишите формулу для графика, показанного на рис. 3-8, который представляет собой преобразование функции квадратного корня из инструментария.

Рисунок 3-8 Анализ

Обратите внимание, что это преобразование изменило домен и диапазон функции. Этот новый граф имеет домен [latex]\text{}\left[1,\infty \right)\text{}[/latex] и диапазон [latex]\text{}\left[2,\infty \right)[ /латекс].

2. Напишите формулу преобразования обратной функции инструментария [latex]\text{}f\left(x\right)=\frac{1}{x}\text{}[/latex], которая сдвигает график на одну единицу вправо и на одну единицу вверх.

Решение

Бесплатный доступ на https://openstax.org/books/precalculus/pages/1-introduction-to-functions

Горизонтальное и вертикальное растяжение/сжатие

Существует печатная версия этих уроков, если она будет вам полезна.

$y = f(x)$ $y = 2f(x)\,$ Вертикальное растяжение; $y$-значения дублируются; точки уходят дальше от $x$-ось	$y = f(x)$ $y = \frac{f(x)}{2}\,$ Вертикальная усадка; $y$-значения уменьшаются вдвое; точки становятся ближе к $x$-ось
Вертикальное растяжение/сжатие изменяет $y$-значения баллов. Преобразования, влияющие на $y$-значения интуитивно понятны.

$y = f(x)$ $y = f(2x)\,$ Горизонтальная усадка; $x$-значения делятся пополам; точки становятся ближе к $y$-ось	$y = f(x)$ $y = f(\frac x2)$ Горизонтальное растяжение; $x$-значения дублируются; точки уходят дальше от $y$-ось
Горизонтальное растяжение/сжатие изменяет $x$-значения баллов. Преобразования, влияющие на $x$-значения являются контринтуитивными.

Вертикальное/горизонтальное растяжение/сжатие обычно изменяет форму графика.

Урок Графические инструменты: Вертикальное и горизонтальное масштабирование в Учебная программа по алгебре II дает подробное обсуждение горизонтального и вертикального растяжения и сжатия.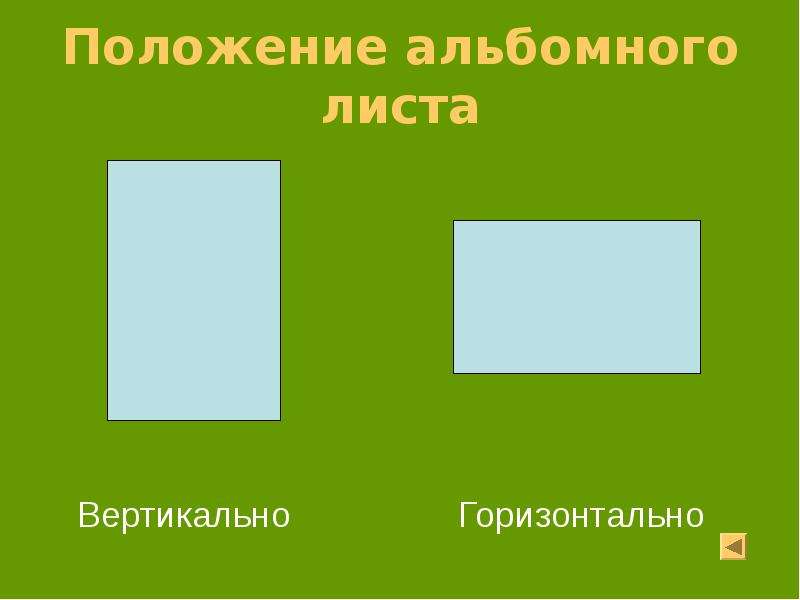 Ключевые понятия повторяются здесь.

Упражнения в этом уроке повторяют упражнения в Графические инструменты: Вертикальное и горизонтальное масштабирование .

Идеи относительно вертикального масштабирования (Растягивание/сжатие)

• Точки на графике $\,y=f(x)\,$ имеют вид $\,\bigl(x,f(x)\bigr)\,.$

  Точки на графике $\,y=3f(x)\,$ имеют вид $\,\bigl(x,3f(x)\bigr)\,. $

  Таким образом, график $\,y=3f(x)\,$ находится путем взятия график $\,y=f(x)\,$ и умножение $y$-значения на $\,3\,.$ Это перемещает точки дальше от $x$-ось, что делает график более крутым.

• Точки на графике $\,y=f(x)\,$ имеют вид $\,\bigl(x,f(x)\bigr)\,.$

  Точки на графике $\,y=\frac13f(x)\,$ имеют вид $\,\bigl(x,\frac13f(x)\bigr)\,. $

  Таким образом, график $\,y=\frac13f(x)\,$ найден взяв график $\,y=f(x)\,$ и умножение $y$-значения по $\,\frac13\,.$ Это перемещает точки ближе к $x$-ось, что делает график более плоским.

• Преобразования с участием $\,y\,$ работают так, как вы ожидаете от них — они интуитивно понятны.

• Вот мыслительный процесс, который вы должны использовать когда вам дан график $\,у=е(х)\,$ и спросил о графике $\,y=3f(x)\,$:

$$ \начать{выравнивать} \text{исходное уравнение:} &\quad y=f(x)\cr \text{новое уравнение:} &\quad y=3f(x) \end{выравнивание} $$

Интерпретация нового уравнения:

$$ \начать{собирать} \overset{\text{новые значения y}}{\overbrace{ \стойка\ \ у\ \ }} \overset{\text{являются}}{\overbrace{ \стойка\ \ =\ \ }} \overset{\text{три раза}\ \ }{\overbrace{ \ стойка \ \ 3 \ \ }} \overset{\text{предыдущие значения y}}{\overbrace{ \стойка\ \ f(x)\ \ }} \конец{собрать} $$

Резюме вертикального масштабирования

Пусть $\,k \gt 1\,.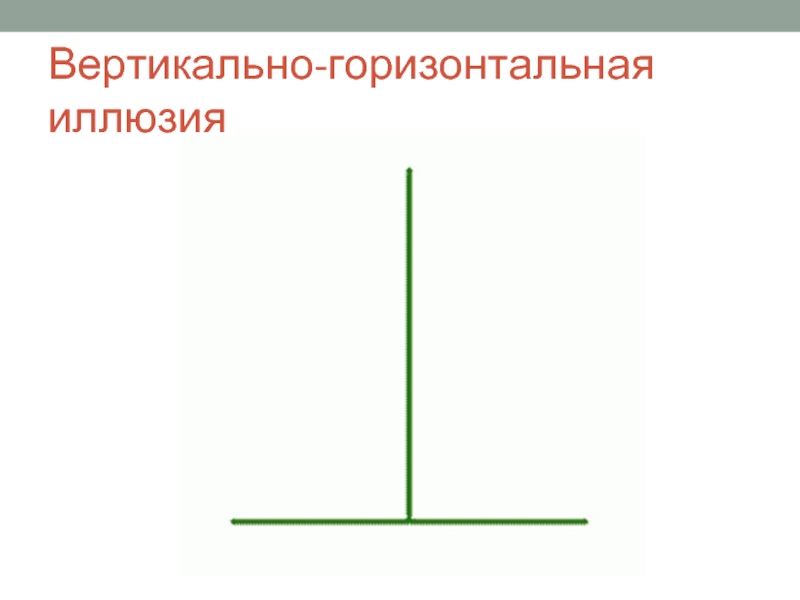 $ Начните с уравнения $\,y=f(x)\,.$ Умножьте предыдущее $y$-значения на $\,k\,$, что дает новое уравнение $\,y=kf(x)\,.$ $y$-значения умножаются на число больше $\,1\,$ чтобы они отошли подальше от $x$-ось. Это делает график более крутым, и называется вертикальным растяжением.

Пусть $\,0 \lt k \lt 1\,.$ Начните с уравнения $\,y=f(x)\,.$ Умножьте предыдущее $y$-значения на $\,k\,$, что дает новое уравнение $\,y=kf(x)\,. $ $y$-значения умножаются на число между $\,0\,$ и $\,1\,$ поэтому они приближаются к $x$-ось. Это делает график более плоским, и называется вертикальной усадкой.

В обоих случаях точка $\,(a,b)\,$ на графике $\,y=f(x)\,$ перемещается в точку $\,(a,kb)\,$ на графике $\,y=kf(x)\,.$

Этот тип преобразования формально называется вертикальное масштабирование (растяжение/сжатие) .

Идеи относительно горизонтального масштабирования (Растягивание/сжатие)

• Точки на графике $\,y=f(x)\,$ имеют вид $\,\bigl(x,f(x)\bigr)\,. $

  Точки на графике $\,y=f(3x)\,$ имеют вид $\,\bigl(x,f(3x)\bigr)\,.$

• Как мы можем найти эти искомые точки $\,\bigl(x,f(3x)\bigr)\,$?

  Во-первых, перейти к делу $\,\цвет{красный}{\bigl(3x\,\,f(3x)\bigr)}\,$ на графике $\,\color{red}{y=f(x)}\,.$

  Эта точка имеет $y$-значение что мы хотим, но это неправильно $x$-значение. Значение $x$ этой точки $\,3x\,$ но желаемое $x$-значение просто $\,x\,.$

  Таким образом, текущий $\color{purple}{x}$-значение необходимо разделить на $\,\color{фиолетовый}{3}\,$. $\color{purple}{y}$-значение остается такой же. Это дает желаемую точку $\,\color{green}{\bigl(x,f(3x)\bigr)}\,. $

  Таким образом, график $\,y=f(3x)\,$ совпадает с графиком $\,y=f(x)\,$ за исключением того, что $x$-значения были разделены на $\,3\,$ (, а не , умноженное на $\,3\,$, как вы могли бы ожидать).

  Обратите внимание, что разделение $x$-значения на $\,3\,$ перемещает их ближе к $y$-ось. Это называется горизонтальной усадкой.

• Преобразования с участием $\,x\,$ НЕ работают так, как вы ожидаете, что они будут работать! Они противоречат интуиции — они противоречат вашей интуиции.

• Вот мыслительный процесс, который вы должны использовать когда вам дан график $\,y=f(x)\,$ и спросил о графике $\,y=f(3x)\,$:

  $$ \начать{выравнивать} \text{исходное уравнение:} &\quad y=f(x)\cr \text{новое уравнение:} &\quad y=f(3x) \end{выравнивание} $$

  $$ \начать{собирать} \text{Интерпретация нового уравнения:}\cr\cr у = е( \overset{\text{заменить $x$ на $3x$}}{\overbrace{ \ \ 3x\ \ }} ) \конец{собрать} $$

  Заменив каждый $\,x\,$ на $\,3x\,$ в уравнении вызывает $x$-значения в графе ДЕЛИТЬСЯ на $\,3\,. $

Краткий обзор горизонтального масштабирования

Пусть $\,k\gt 1\,.$ Начните с уравнения $\,y=f(x)\,.$ Замените каждый $\,x\,$ на $\,kx\,$, чтобы дают новое уравнение $\,y=f(kx)\,.$ Это вызывает $x$-значения на графе, подлежащем ДЕЛЕНИЮ на $\,k\,$ который перемещает точки ближе к $y$-ось. Это называется горизонтальной усадкой. Точка $\,(a,b)\,$ на графике $\,y=f(x)\,$ перемещается в точку $\,(\frac{a}{k},b)\,$ на графике $\,y=f(kx)\,. $

Кроме того:

Пусть $\,k\gt 1\,.$ Начните с уравнения $\,y=f(x)\,.$ Замените каждый $\,x\,$ на $\,\frac{x}{k}\,$, чтобы задайте новое уравнение $\,y=f(\frac{x}{k})\,.$ Это вызывает $x$-значения на графе, который нужно УМНОЖИТЬ на $\,k\,$ который перемещает точки дальше от $y$-ось. Это называется горизонтальной растяжкой. Точка $\,(a,b)\,$ на графике $\,y=f(x)\,$ перемещается в точку $\,(ka,b)\,$ на графике $\,y=f(\frac{x}{k})\,. $

Этот тип преобразования формально называется горизонтальное масштабирование (растяжение/сжатие) .

Различные слова, используемые для разговора Преобразования с участием $\,y\,$ и $\,x\,$

Обратите внимание, что разных слов используются, когда речь идет о преобразованиях с участием $\,y\,$ и преобразования с участием $\,x\,.$

Для преобразований с участием $\,у\,$ (то есть преобразования, которые изменяют $y$-значения точек), мы говорим:

СДЕЛАЙТЕ ЭТО к предыдущему $y$-значение

Для преобразований с участием $\,х\,$ (то есть преобразования, которые изменяют $x$-значения точек), мы говорим:

ЗАМЕНИТЬ предыдущий $x$-значения по $\ldots$

Убедитесь, что вы видите разницу!

Вертикальное масштабирование:
Переход от $\,у=е(х)\,$ к $\,y = kf(x)\,$  для  $\,k\gt 0$

Горизонтальное масштабирование:
Переход от $\,у = f(x)\,$ к $\,y = f(kx)\,$  для  $\,k\gt 0$

Убедитесь, что вы видите разницу между (скажем) $\,у = 3f(x)\,$ и $\,y = f(3x)\,$!

В случае $\,y = 3f(x)\,$ $\,3\,$ находится «снаружи»: мы опускаем $\,x\,$ в ячейку $\,f\,$, получение соответствующего вывода, и , затем , умноженное на $\,3\,. $ Это вертикальная растяжка.

В случае $\,y = f(3x)\,$ $\,3\,$ находится «внутри»: мы умножаем $\,x\,$ на $\,3\,$ перед , опуская его в ящик $\,f\,$. Это горизонтальная усадка.

Примеры

Вопрос: Начните с $\,y = f(x)\,.$ Сделайте вертикальную растяжку: $y$-значения на графике следует умножить на $\,2\,.$ Что такое новое уравнение?

Решение: Это трансформация, включающая $\,у\,$; это интуитивно понятно. Вы должны умножить предыдущее $y$-значения на $\,2\,.$ Новое уравнение: $\,y = 2f(x)\,$

Вопрос: Начните с $\,y = f(x)\,.$ Сделайте горизонтальную растяжку: $x$-значения на графике должно быть умножено на $\,2\,.$ Что такое новое уравнение?

Решение: Это трансформация, включающая $\,х\,$; это нелогично. Вы должны заменить каждый $\,x\,$ в уравнении через $\,\frac{x}{2}\,.$ Новое уравнение: $\,y = f(\frac{x}{2})\,$ 93\,.